Let us go back to Terence Tao’s Solving Mathematical Problems, for another exercise. As done in a previous post, I would like to show an alternative solution to a problem the author proposes, that I think is instructive and considerably fast, once the appropriate perspective on the situation is taken.
Let \(ABFE\) be a rectangle and \(D\) be the intersection of the diagonals \(AF\) and \(BE\). A straight line through \(E\) meets the extended line \(AB\) at \(G\) and the extended line \(FB\) at \(C\) so that \(DC \cong DG\). Show that \[\frac{\overline{AB}}{\overline{FC}} = \frac{\overline{FC}}{\overline{GA}} = \frac{\overline{GA}}{\overline{AE}}.\tag{1}\label{eq3702:1}\]
Here is a picture that shows the initial situation.
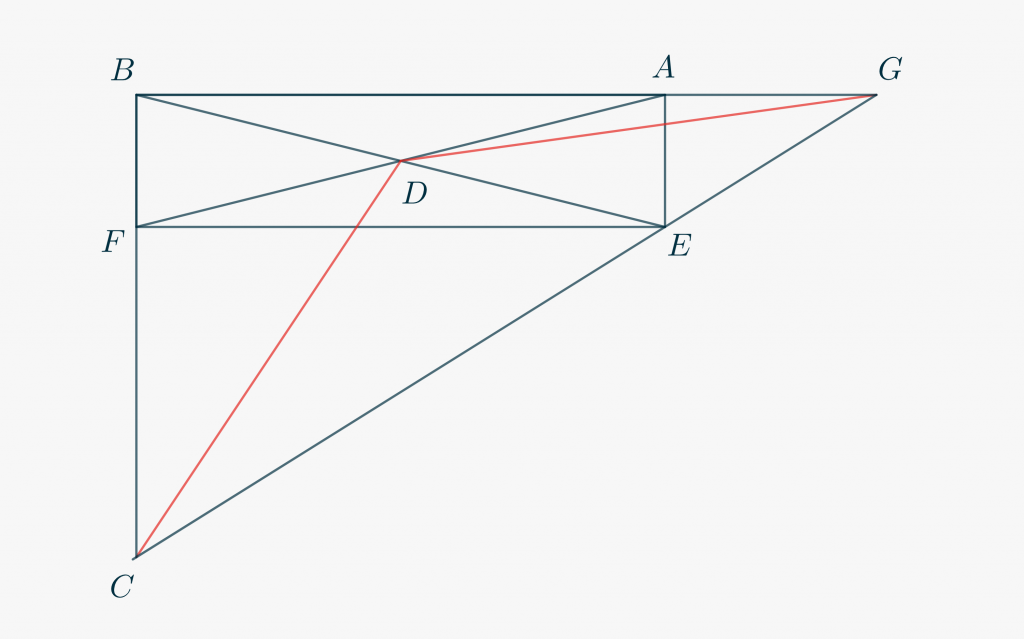
Now, looking at \eqref{eq3702:1} as proportions, you can notice that the thesis is equivalent to stating that \(FC\) is mean proportional between \(AB\) and \(GA\), and \(GA\) is mean proportional between \(FC\) and \(AE\). This, in turn, should make you think of the Geometric Mean Theorem, whose demonstration would require the presence of some right-angled triangles; namely, a right-angled triangle with hypotenuse congruent to \(AB + GA \cong BG\) and altitude congruent to \(FC\), and a right-angled triangle with hypotenuse congruent to \(FC + AE\) and altitude congruent to \(GA\). Before reading further, try to find this configuration yourself starting from the Figure above (it should suffice to introduce just one additional point).
I proceeded as follows.
- Extend \(CD\) and \(AE\) so that they intersect at \(C’\).
- Use the fact that \(BC \parallel AE\) and ASA criterion on \(\triangle FDC\) and \(\triangle C’DA\) to show that \(C’A \cong FC\). Conclude also that \(CD \cong C’D\).
The situation now should be like the one shown below.
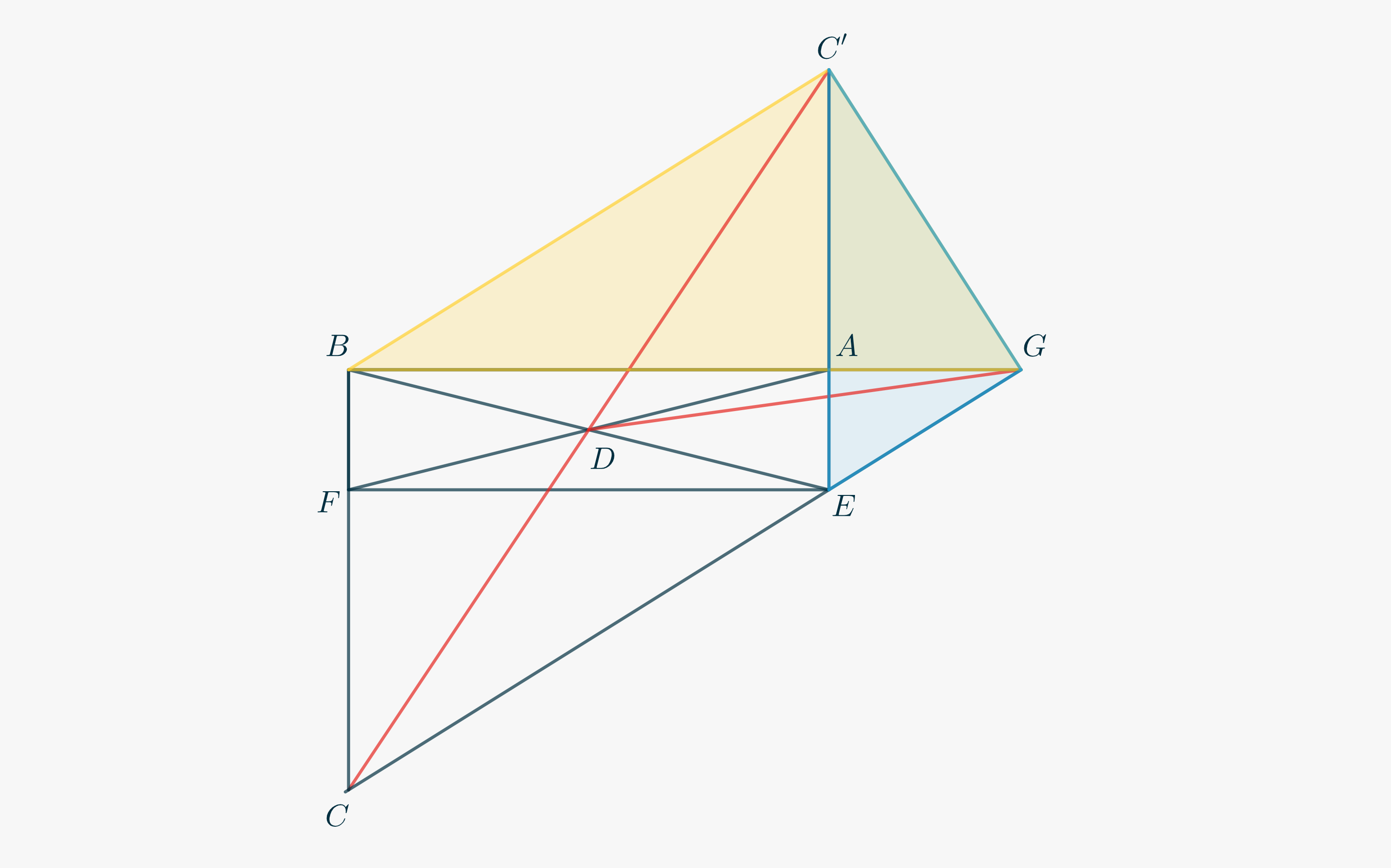
From what was stated above, the thesis is reached once we have proved that \(\triangle BC’G\) and \(\triangle C’GE\) are right-angled. Then, in fact, \eqref{eq3702:1} is a consequence of the Geometric Mean Theorem. How would you complete the proof? Read further if you need some hints.
Here is my approach.
- Use the hypotheses and the above demonstration to show that \(\triangle CC’G\) is inscribed in a semicircle with center in \(D\). Deduce that \(CG\perp C’G\).
- Observe the quadrilateral \(BCEC’\) and, noting that its diagonals bisect, prove that it is a parallelogram. Conclude that \(BC’ \parallel CG\) and hence \(BC’ \perp C’G\).
