We take again inspiration from the Putnam competition, for an exercise on continuity and differentiability of real fuctions obtained by “stretching” a basic replica.
Let us start from problem A.6. of the 1996 Putnam competition, to which we will add a little twist.
Let \(c>0\) be a constant. Give a complete description, with proof, of the set of all continuous functions \(f: \Bbb R \to \Bbb R\) such that \(f(x) =f(x^2+c)\) for all \(x \in\Bbb R\).
The first thing it is interesting to notice is that the function \(f\) must be even, since \[f(-x) = f((-x)^2+x) = f(x^2+c) = f(x).\]
This allows us to find first a function \(f^+ : \Bbb R^+ \to \Bbb R\) that satisfies the required condition, and then define \(f\) as \[f(x) = f^+(|x|).\].
This stated, we are interested in examining what happens when we map the generic point \(x\) in the domain of the function to the point \(x^2+c\). The behavior of this map depends the on value taken by \(c\).
Let us first consider the case in which the map \(x \mapsto x^2+c\) always produces an increase in the value of the independent variable. This happens if \(x^2-x+c>0\) for all \(x\), that is when \(c>\frac14.\). In this case any sequence starting with \(b_0\geq 0\) and iteratively defined as \[ b_k=(b_{k-1})^2+c\] for \(k=1,2,\dots\) is divergent.
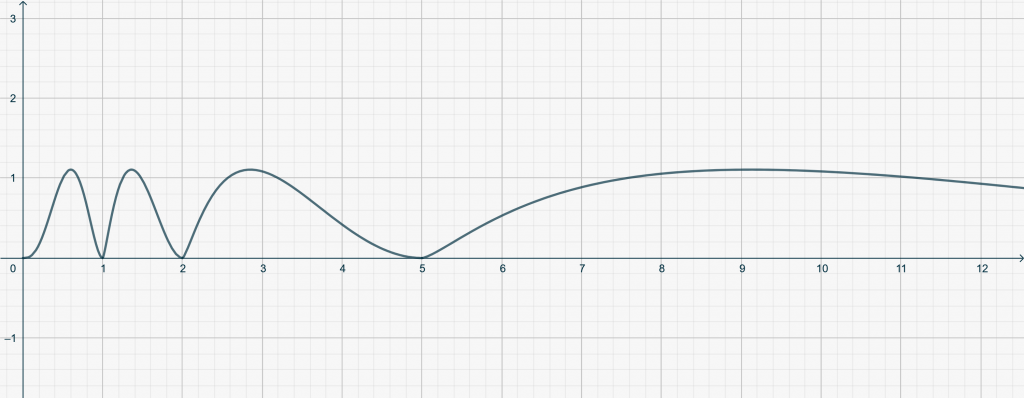
As a result, we can construct \(f^+\) by starting with any continuous function \[f_0 : [0,c] \to \Bbb R\] such that \(f_0(0) = f_0(c)\) and iteratively define \[f^+(x) = \begin{cases} f_0(x) & ( a_0 \leq x < a_1)\\f_1(x) = f_0(\sqrt{x-c}) & (a_1 \leq x < a_2)\\ f_2(x) = f_1(\sqrt{x-c}) & (a_2 \leq x < a_3)\\ \vdots & \vdots\\ f_k(x) = f_{k-1}(\sqrt{x-c}) & (a_k \leq x < a_{k+1}) \\ \vdots & \vdots \end{cases}\tag{1}\label{eq3795:1}\] with \(a_0 = 0\), and \(a_k = (a_{k-1})^2+c\) for \(k=1,2,\dots\). Below an example with \(c = 1\) and \[f_0(x) = x-x^2.\]
If we take \(c = \frac14\), the situation changes drastically. Let \[f\left(\frac12\right) = K\] and suppose there exists \(\overline x\) such that \(f(\overline x ) \neq K\).
If \(0\leq \overline x < \frac12\), then the sequence defined as \(b_0 = \overline x\) and \[b_k = (b_{k-1})^2+\frac12\] for \(k=1,2,\dots\) converges to \(\frac12\) and is such that \[f(b_k) = f(\overline x)\neq K = f\left(\frac12\right). \] for all \(k=0,1,2\dots\). Explain why this contradicts continuity of \(f\).
Similarly, if \(\overline x > \frac12\), you can use the sequence \(d_0 = \overline x\) and \[d_k = \sqrt{d_{k-1}-\frac12}\] for \(k=1,2,\dots\), to reach again a contradiction.
We can conclude that in this case the only functions that satisfy the condition are the constant functions.
As an exericise, use the strategy above to conclude that the constant functions are the only solution to our problem whenever \(0 < c \leq \frac14\).
The example given in the Figure above satisfies the requirements, but is not differentiable. So we could ask ourselves if there are solutions to the original problem that are also differentiable.
We refer to the same notation used above. Suppose such \(f\) exists and let us assume WLOG that \(f(0) = 0\).
We first necessarily require \(f_0\) to be differentiable in \([0,c]\). In the following steps you will see what other conditions have to be added to \(f_0\), in order for \(f^+\), and therefore \(f\), to be differentiable in \(\Bbb R\).
- From the even simmetry of \(f\) conclude that \(f’_0(0)\) must be equal to \(0\). Therefore \(f’_0(c)\) must also be equal to \(0\).
- Show that \[\lim_{x \to c^+}\frac{f_1(x)}{x-c}=\lim_{t\to 0^+}\frac{f_0(t)}{t^2}.\] Conclude that if must be \[f_0(x) = o(x^2) \ \ \mbox{for} \ \ x \to 0^+.\tag{2}\label{eq3795:2}\] for \(f\) to be differentiable in \(c\). Note that having well defined and null second derivative in \(0\) is a sufficient but not necessary condition for \eqref{eq3795:2} to hold true.
- Show that \[\lim_{x\to (c^2+c)^-} \frac{f_1(x)}{x-c^2-c}=\lim_{t\to c^-}\frac{f_0(t)}{(t-c)(t+c)}.\] Conclude that we also need \(f_0(x)\) to be (right) differentiable in \(c\), with differential coefficient equal to \(0\).
- Is differentiability inherited also by the other replicas \(f_k\), with \(k=2,3,\dots\)? The answer is on the affirmative. Recall the definition of \(a_k\) given in \eqref{eq3795:1} and draw this conclusion by the follwing limits: \[\lim_{x\to a_k^+}\frac{f_k(x)}{x-a_k}=\lim_{t\to a_{k-1}^+}\frac{f_{k-1}(t)}{(t+a_{k-1})(t+a_{k-1})}\] and\[\lim_{x\to a_{k+1}^-}\frac{f_k(x)}{x-a_{k+1}}=\lim_{t\to a_k^-}\frac{f_{k-1}(t)}{(t-a_k)(t+a_k)}.\]
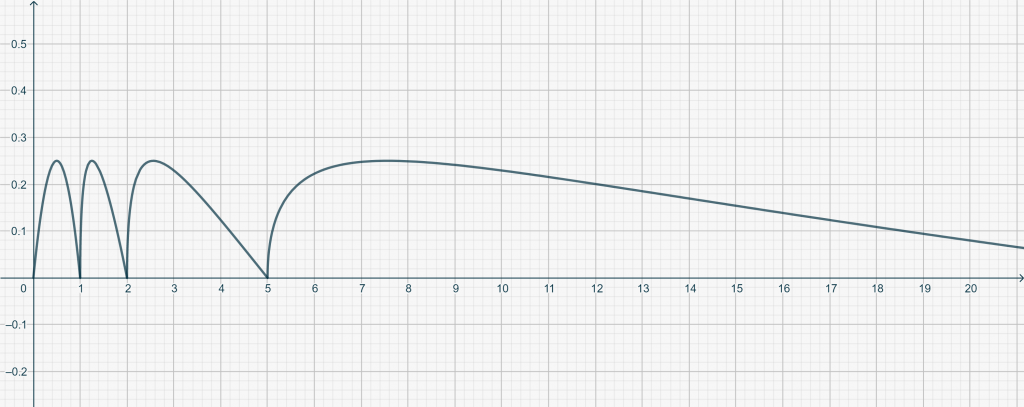
In the example below, we chose \(c=1\) and \[f_0(x) = 32x^3(x-1)^2.\]