Torniamo al testo “Solving Mathematical Problems” di Terence Tao per un altro esercizio. Come in un precedente post, vi espongo una soluzione alternativa a un problema proposto dall’autore, perché mi sembra particolarmente istruttiva e rapida, una volta che si assume la “giusta” prospettiva.
Sia \(ABFE\) un rettangolo e sia \(D\) l’intersezione tra le diagonali \(AF\) e \(BE\). Una linea retta passa per \(E\), intersecando l’estensione di \(AB\) in \(G\) e l’estensione di \(FB\) in \(C\), in modo tale che \(DC \cong DG\). Dimostrare che \[\frac{\overline{AB}}{\overline{FC}} = \frac{\overline{FC}}{\overline{GA}} = \frac{\overline{GA}}{\overline{AE}}.\tag{1}\label{eq3758:1}\]
Ecco un’immagine della situazione descritta nel testo.
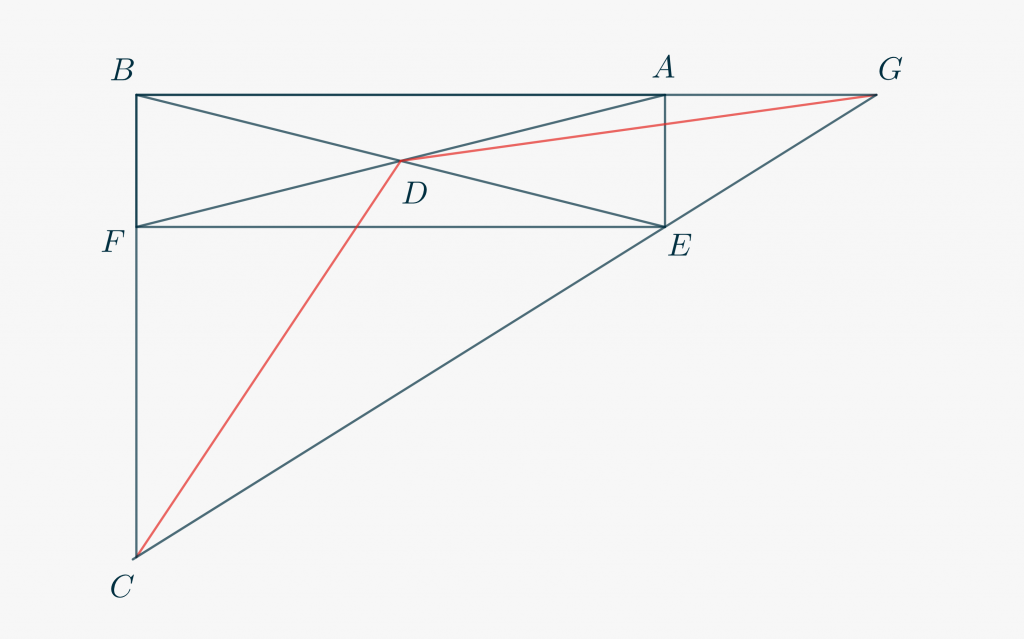
Ora, interpretando la \eqref{eq3758:1} in forma di proporzione, puoi notare come la tesi sia equivalente all’affermazione che \(FC\) è medio proporzionale tra \(AB\) e \(GA\), e che \(GA\) è medio proporzionale tra \(FC\) e \(AE\). Ciò dovrebbe farti pensare al Secondo Teorema di Euclide, il cui utilizzo richiederebbe la presenza di triangoli rettangoli con opportune ipotenuse e altezze (relative all’ipotenusa); più precisamente ci occorrono: un triangolo rettangolo con ipotenusa equivalente a \(AB + GA \cong BG\) e altezza congruente a \(FC\), e un triangolo rettangolo con ipotenusa congruente a \(FC + AE\) e altezza congruente a \(GA\). Prima di proseguire la lettura, prova ad ottenere la corretta “configurazione” partendo dalla Figura qui sopra (dovrebbe esserti sufficiente introdurre un solo punto addizionale).
Io ho proceduto nel modo seguente.
- Estendi \(CD\) e \(AE\) in modo che le estensioni si intersechino in \(C’\).
- Usa il fatto che \(BC \parallel AE\) ed il secondo criterio di congruenza su \(\triangle FDC\) e \(\triangle C’DA\) per dimostrare che \(C’A \cong FC\). Osserva inoltre che \(CD \cong C’D\).
La situazione dovrebbe ora apparire come nella Figura qui sotto.
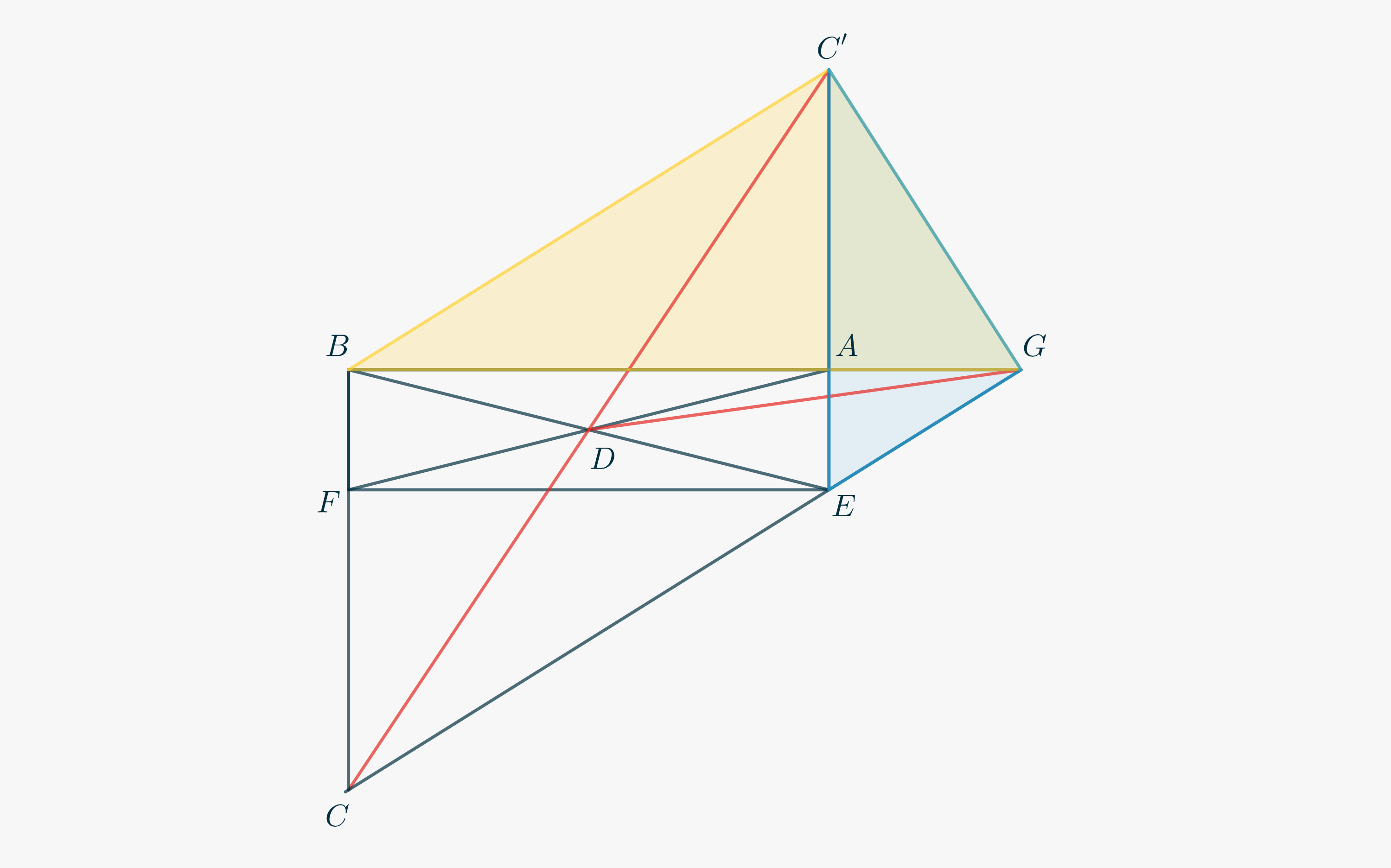
Per quanto detto, la tesi è raggiunta una volta che si è dimostrato che \(\triangle BC’G\) e \(\triangle C’GE\) sono triangoli rettangoli. Infatti, a questo punto \eqref{eq3758:1} è una conseguenza del Secondo Teorema di Euclide. Come puoi completare la dimostrazione? Prosegui la lettura se hai bisogno di qualche suggerimento.
Ecco l’approccio che ho seguito.
- Usa le ipotesi e la dimostrazione precedente per mostrare che il triangolo \(\triangle CC’G\) è inscritto in una semicirconferenza centrata in \(D\). Deduci che \(CG\perp C’G\).
- Osserva il quadrilatero \(BCEC’\) e, notando che le sue diagonali si bisecano, concludi che si tratta di un parallelogramma. Concludi che \(BC’ \parallel CG\) e quindi \(BC’ \perp C’G\).