Theorem. Let \(f\) be a real function, which is differentiable up to order \(n\) in \(c \in \Bbb R\), for some positive integer \(n\). Suppose that \(f^{(n)}(c) \neq 0\), and that all preceeding derivatives (if any) are null in \(c\). Then \(c\) is a local extremum if and only if \(n\) is even.
In the following, the notation \(f^{(k)}(x)\), for \(k>0\) is used to identify the \(k\)-th order derivative of \(f\) in \(x\), and, for \(k=0\), \(f^{(0)}(x) = f(x)\). We will also assume, WLOG, that \(c=0\), \(f(0)=0\), and \(f^{(n)}(0)>0\).
Since we have information only about the \(n\)-th order derivative in \(c\) and not in a neighborhood of \(c\), we cannot make use of Taylor’s Theorem. That is the main reason why I thought to propose to the reader the proof of this assertion. However, if we use the definition of derivative given for example in Rudin’s Principles of Mathematical Analysis (def. 5.1, page 103), for \(k=1,2,\dots\), the existence of \(f^{(k)}(c)\) implies the existence of \(f^{(k-1)}(x)\) in a whole interval containing \(c\). This will allow us to make approprate use of the Mean Value Theorem.
First observe that \[\lim_{x\to 0}\frac{f^{(n-1)}(x)}{x} = f^{(n)}(0) > 0,\]implying that there exists a neighborhood \(\mathcal N\) of \(0\) such that \[\frac{f^{(n-1)}(x)}{x} > 0,\tag{1}\label{eq3649:1}\]for all \(x \in \mathcal N\setminus \{0\}\). If \(n=1\), we are done, since by \eqref{eq3649:1} \(f^{(0)}(x)=f(x)\) does not have a local extremum in \(0\).
If \(n>1\), from \eqref{eq3649:1} we can conclude that \[f^{(n-2)}(x)>0\tag{2}\label{eq3649:2}\] for all \(x\in \mathcal N\setminus \{0\}\). We can prove this assertion by contradiction. Suppose in fact there is \(\overline x \in \mathcal N\setminus \{0\}\) such that \(f^{(n-2)}(\overline x)\leq 0\). Then, by the Mean Value Theorem we would find \(\xi\) such that \[f^{(n-1)}(\xi) = \frac{f^{(n-2)}(\overline x)}{\overline x}.\] If \(\overline x >0\), then \(0< \xi <\overline x\), and \(f^{(n-1)}(\xi) \leq 0\). If, instead \(\overline x < 0\), then \(\overline x < \xi < 0\) and \(f^{(n-1)}(\xi) \geq 0\). Both situations contradict \eqref{eq3649:1}.
If \(n=2\), our conclusion is reached, since from \eqref{eq3649:2} it follows that \(0\) is a local minimum (this depends on the choice we have made to let \(f^{(n)}(0) > 0\), of course).
If \(n>2\), note that \eqref{eq3649:2} implies that \(f^{(n-3)}(x)\) is strictly monotonic in \(\mathcal N\). Together with the condition \(f^{(n-3)}(0) = 0\), this yields \[\frac{f^{(n-3)}(x)}{x} > 0\]for all \(x \in \mathcal N \setminus \{0\}\).
Now it is straightforward to proceed further and show that \[f^{(n-2k)}(x)>0 \ \ \mbox{for} \ \ k=0,1\dots ,\left\lfloor \frac{n}2\right\rfloor-1\] for all \(x \in \mathcal N \setminus \{0\}\), and that \[\frac{f^{(n-2k-1)}(x)}{x} > 0\ \ \mbox{for} \ \ k=0,1,\dots ,\left\lfloor \frac{n}2\right\rfloor-1\] for all \(x \in \mathcal N \setminus \{0\}\). The last two assertions easily yield our thesis.
Here are some interesting examples. The first one is taken from Robert Burn’s Numbers and Functions. Take \[f(x) = \begin{cases}x + 2x^2 \cos\left(\frac1{x}\right) & (x\neq 0) \\ 0 & (x=0).\end{cases}\] This function has first derivative equal to \(1\) in \(0\) (use the definition of derivative!). However \(f(x)\) is not increasing in any neighborhood of \(0\). You can show in fact that \(f\left(\frac1{2k\pi}\right) > f\left(\frac1{(2k-1)\pi}\right)\) for any \(k =1,2,\dots\). Note that \(f'(x)\) is not continuous in \(0\).
The above example can be generalized by\[f(x) = \begin{cases}\frac{ax^n} {n!} + x^{2n}\cos\left(\frac1{x}\right) & (x\neq 0)\\ 0 & (x=0),\end{cases}\]where \(f^{(k)}(0) = 0\) for \(0<k<n\) and \(f^{(n)}(0) = a\), with \(f^{(n)}(x)\) discontinuous in \(0\).
Note that the Theorem requires that there exists at least one non-null derivative.
If all derivatives up to a certain order \(n-1\) exist and are zero in \(c\), and the \(n\)-th order derivative does not exist, no conclusion can be drawn. Take as an example \[f(x) = \begin{cases} x^{2(n-1)}\left[2 + \cos \left(\frac1{x}\right)\right] & (x\neq 0) \\ 0 & (x=0). \end{cases}\tag{3}\label{eq3649:3}\]The above function, for any \(n>1\), has a (global) minimum in \(0\), it has \(f^{(k)}(0) = 0\) for \(0<k<n\), and \(f^{(n)} (x)\) is not defined in \(0\) (see Figure below).
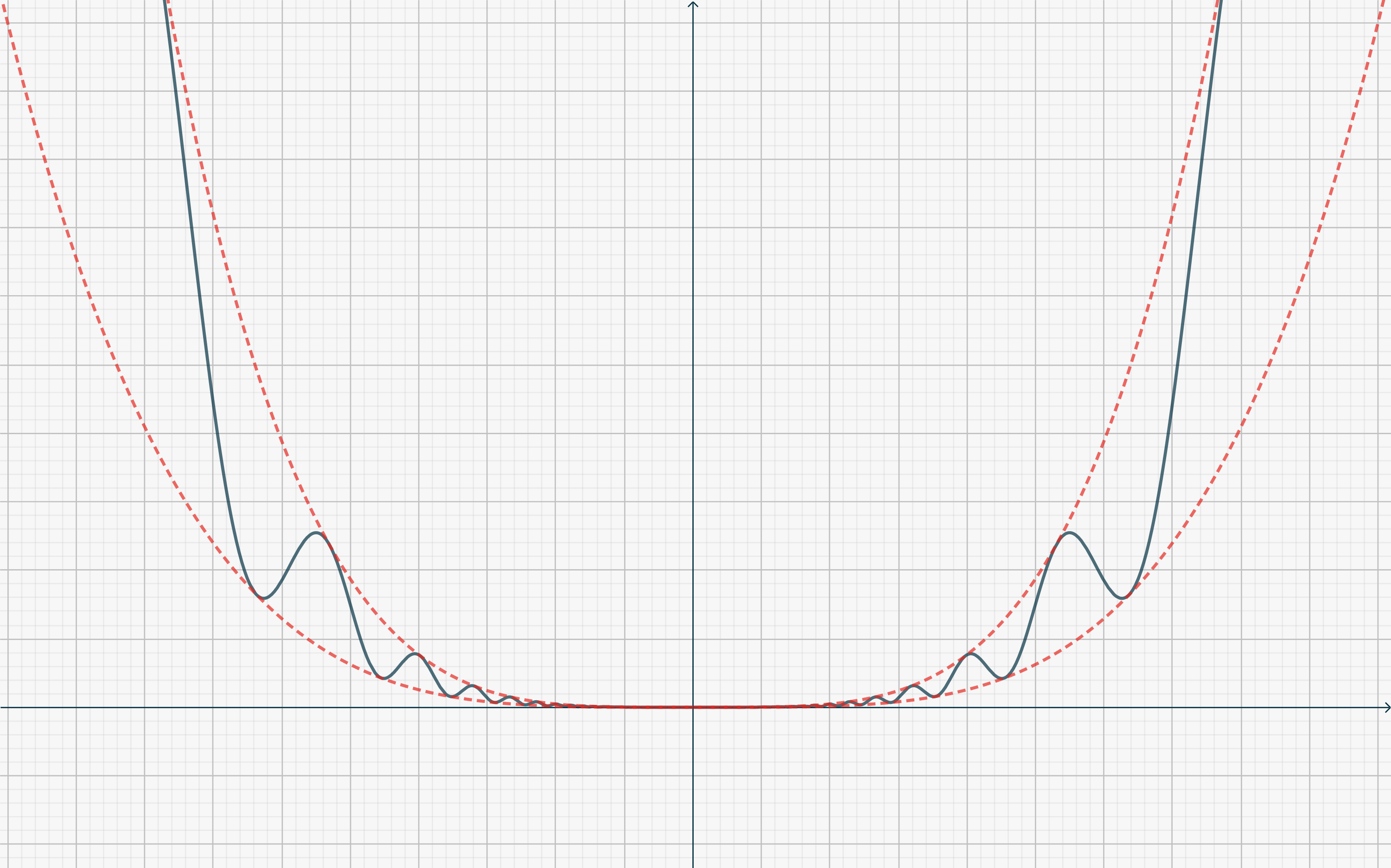
Further exercise.
- Show that, for \(x \neq 0\), the derivative of function \eqref{eq3649:3} can be upper bounded as follows.\[f'(x) \leq x^{2n-4}\sin\left(\frac1{x}\right) + 6(n-1)x^{2n-3}.\]
- Deduce that for \(x = \frac1{2k\pi -\frac{\pi}2}\), with \(k\) integer and \(k>\frac14 + \frac{3(n-1)}{\pi}\), \(f'(x)\) is negative.
- Conclude that \(f(x)\) is not monotonically increasing in any right neighborhood of \(0\).
On the same track, for \(n>1\), the function\[f(x) = \begin{cases} x^{2n-1}\left[2 + \cos \left(\frac1{x}\right)\right] & (x\neq 0) \\ 0 & (x=0). \end{cases}\] (which does not have a local extremum in \(0\), being an odd function) has null (and continuous) derivatives in \(0\) up to order \(n-1\), whereas the \(n\)-th derivative in \(0\) does not exist. A picture of the situation in this case is shown below.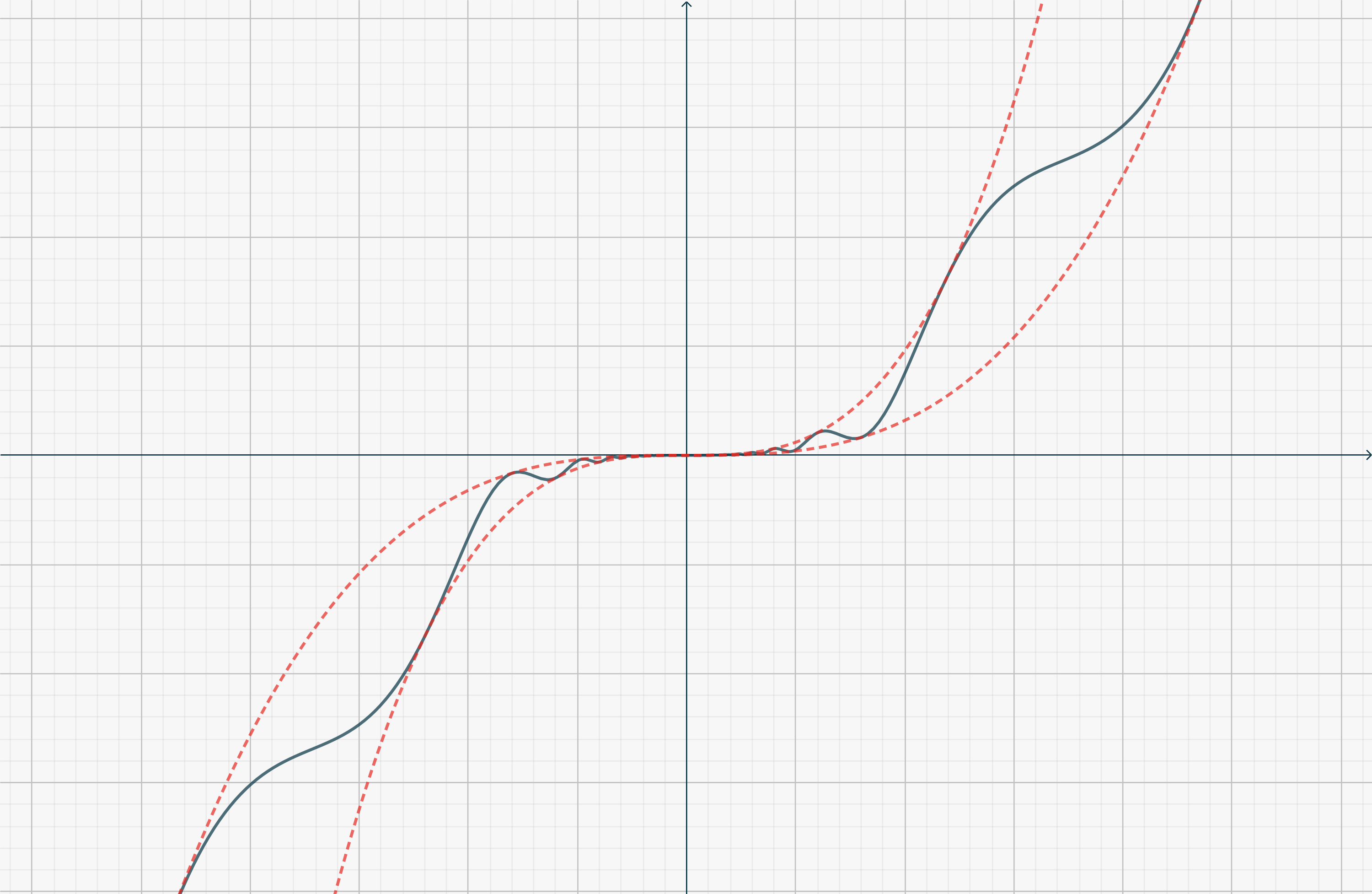
Similarly, if all derivatives are null in \(c\), then no conclusion can be drawn about \(c\) being a local extremum or not. Consider for example \[f(x) = \begin{cases} e^{-\frac1{x^2}} & (x\neq 0) \\ 0 & (x=0),\end{cases}\]and\[f(x) = \begin{cases} \frac{x}{|x|}e^{-\frac1{x^2}} & (x\neq 0) \\ 0 & (x=0).\end{cases}\]
