I found the following problem on Terenece Tao’s “Solving Mathematical Problems”. I propose, here, a synthetic approach based on simple Euclidean geometry concepts, instead of trigonometry, beacuse I think it is illuminating on the “meaning” of the results.
In triangle \(\triangle ABC\) the bisector of the angle \(\angle ABC\) meets \(AC\) in \(D\), and the angle bisector of \(\angle ACB\) meets \(AB\) in \(E\). These bisectors meet at \(O\). Suppose that \(OD \cong OE\). Prove that \(\measuredangle BAC = 60^\circ\) or that \(\triangle ABC\) is isosceles, or both.
It might be useful to recall that a triangle is equilateral if and only if the internal bisectors are also altitudes. As a matter of fact, it is straightforward to verify (do it as an exercise) that if the orthogonal projections of \(O\) on \(AC\) and \(AB\) (call them \(H\) and \(K\)) coincide with \(D\) and \(E\) respectively, then \(\triangle ABC\) is equilateral, which is equivalent to say that both conditions in the problem statement are met.
This suggets to further investigate the behavior of these projections, in the more general situation. We can exploit the properties of the incenter \(O\), together with the fact \(OE \cong OD\). Before reading further, you can gather all the useful information by yourself.
You may have noticed that the the right-angled triangles \(\triangle ODH\) and \(\triangle OEK\) are congruent (fill in the details; which congruence criterion can you use?). In particular we have \(DH \cong EK\), \(\angle DOH \cong \angle EOK\), and \(\angle ODH \cong \angle OEK\).
Case 1 – \(H\) and \(K\) “fall” on the same side with respect to \(D\) and \(E\).
Then either \(AD \cong AH – DH\) and \(AE \cong AK – EK\) (as in the figure below), or \(AD \cong AH + DH\) and \(AE \cong AK + EK\). In either case, we have \(AD \cong AE\).
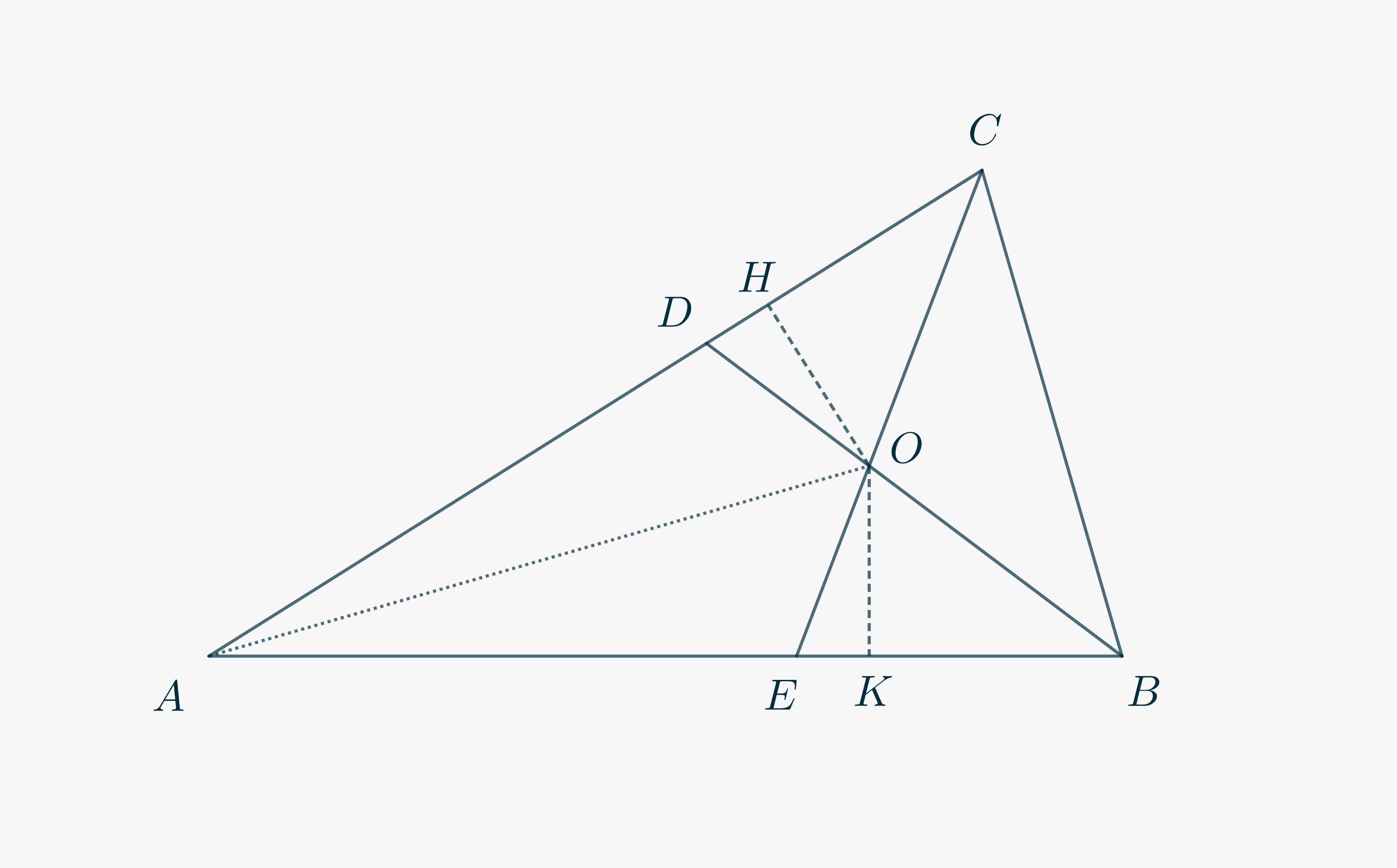
Concentrate now on triangles \(\triangle ACE\) and \(\triangle ADB\). Can you use your results to show that \(AC\cong AB\)?
Case 2 – \(H\) and \(K\) “fall” on opposite sides with respect to \(D\) and \(E\).
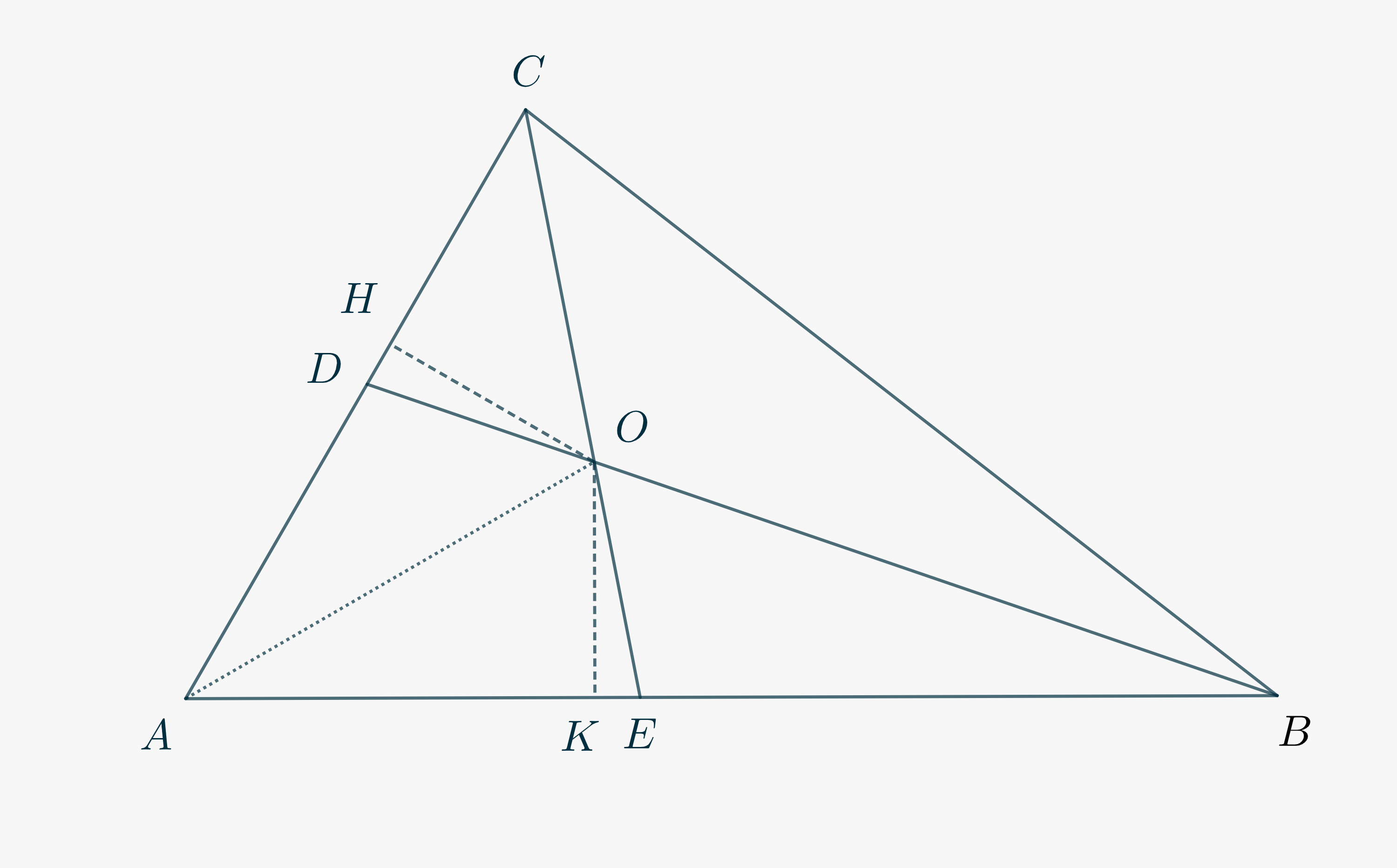
Can you state that \[\measuredangle DOE = \measuredangle HOK?\tag{1}\label{eq3589:1}\] Why is it so?
Consider triangle \(\triangle COB\) and conclude that\[\measuredangle DOE = \measuredangle COB = 180^\circ – \frac{\measuredangle ABC + \measuredangle ACB}2.\tag{2} \label{eq3589:2}\]
Consider now the quadrilateral \(\square AHOK\). Why do we have\[\measuredangle HOK = 180^\circ – \measuredangle BAC? \tag{3}\label{eq3589:3}\]
Thanks to \eqref{eq3589:1}, you can now equate \eqref{eq3589:2} and \eqref{eq3589:3}. This, together with the obvious fact \( \measuredangle ABC + \measuredangle ACB = 180^\circ – \measuredangle BAC\), will lead to the desired result, i.e. \(\measuredangle BAC = 60^\circ\).
