While solving some exercises for my students, I bumped into the following sub-problem: given a divergent sequence \((a_n)\), such that \((a_{n+1} – a_n)\) converges to \(1\), can we state that \(a_n \sim n\) for \(n \to +\infty\)? The answer to the quesiton, as I propose it, requires some drawing, and it is useful to practice the definition of limit.
Theorem. Let \((a_n\)) be a diverging sequence such that\[\lim_{n\to +\infty} (a_{n+1}-a_n) = 1,\tag{1}\label{eq3531:1}\] then we have\[\lim_{n\to +\infty} \frac{a_n}{n} = 1.\]
For any given \(\varepsilon > 0\), we need to find \(N_\varepsilon>0\) such that, for all \(n> N_\varepsilon\), \[\left|\frac{a_n}{n}-1\right|<\varepsilon\tag{2}\label{eq3531:2}.\]
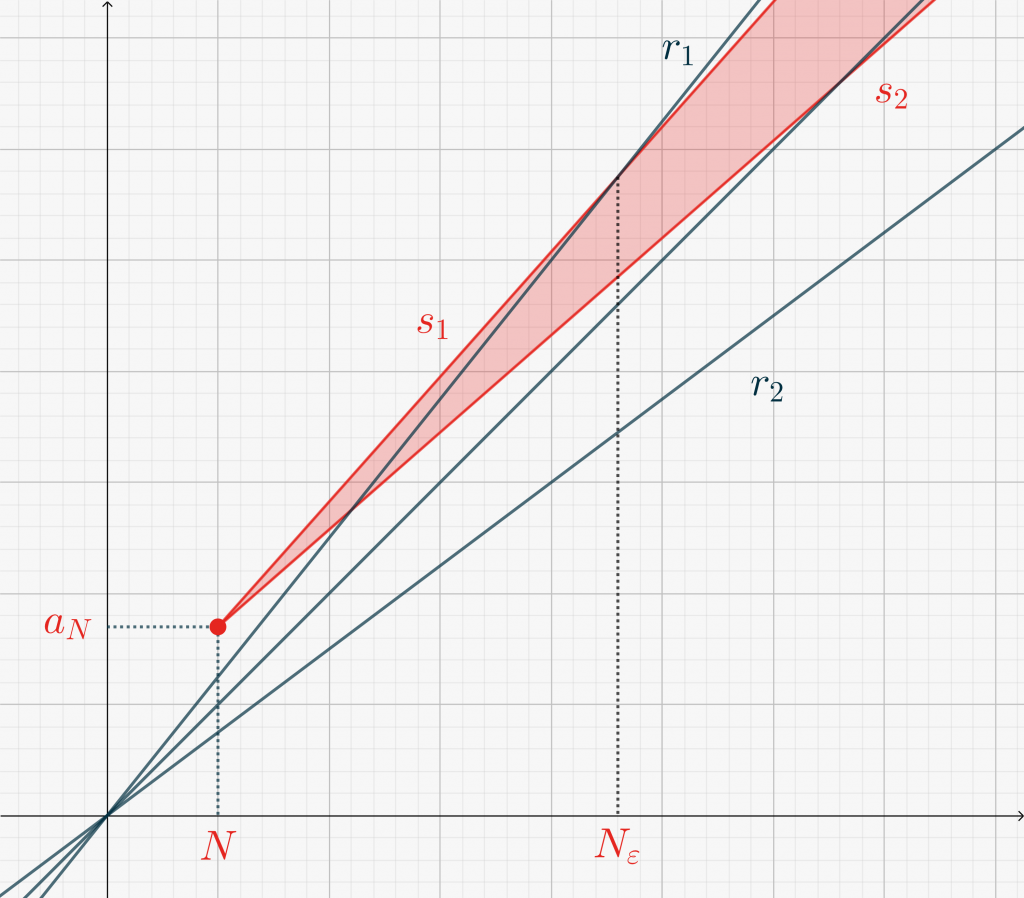
Note that \eqref{eq3531:2} is equivalent to stating that, for large enough \(n\), the points \(P_n(n,a_n)\) must lie between the straight lines \(r_1\) and \(r_2\) with equations \(y=(1+\varepsilon) x\) and \(y=(1-\varepsilon) x\), respectively. Let us call this region \(\mathcal Q_\varepsilon\).
By \eqref{eq3531:1}, we can state that there exists \(N\) such that, for \(k\geq N\), \[a_k+1-\frac{\varepsilon}2 < a_{k+1}< a_k+1+\frac{\varepsilon}2.\tag{3}\label{eq3531:3}\]
Repeated application of \eqref{eq3531:3} for \(k=N,N+1,\dots,N+n\), yields\[a_N + n – n\frac{\varepsilon}2< a_{N+n} < a_N + n + n\frac{\varepsilon}2,\tag{4}\label{eq3531:4}\] valid for all \(n>0\). Again it is useful to interpret \eqref{eq3531:4} geometrically. The above equation states that for \(n>0\) the points \(P_{N+n}(N+n,a_{N+n})\) are contained within the straight lines with equations \[s_1 : \ \ y=(x-N)\left(1+\frac{\varepsilon}2\right) + a_N\] and\[s_2 : \ \ y=(x-N)\left(1-\frac{\varepsilon}2\right) + a_N\](this corresponds to the shaded area in the Figures below).
The slopes of these lines have been chosen in such a way that, if \(P_N \in \mathcal Q_\varepsilon\), so are all points \(P_n\) for \(n>N\). This allows us to simply take \(N_\varepsilon = N\). See Figure below. Note that in this case the intersections of lines \(r_1\) and \(r_2\) with \(s_1\) and \(s_2\) all occur at \(x < N\).
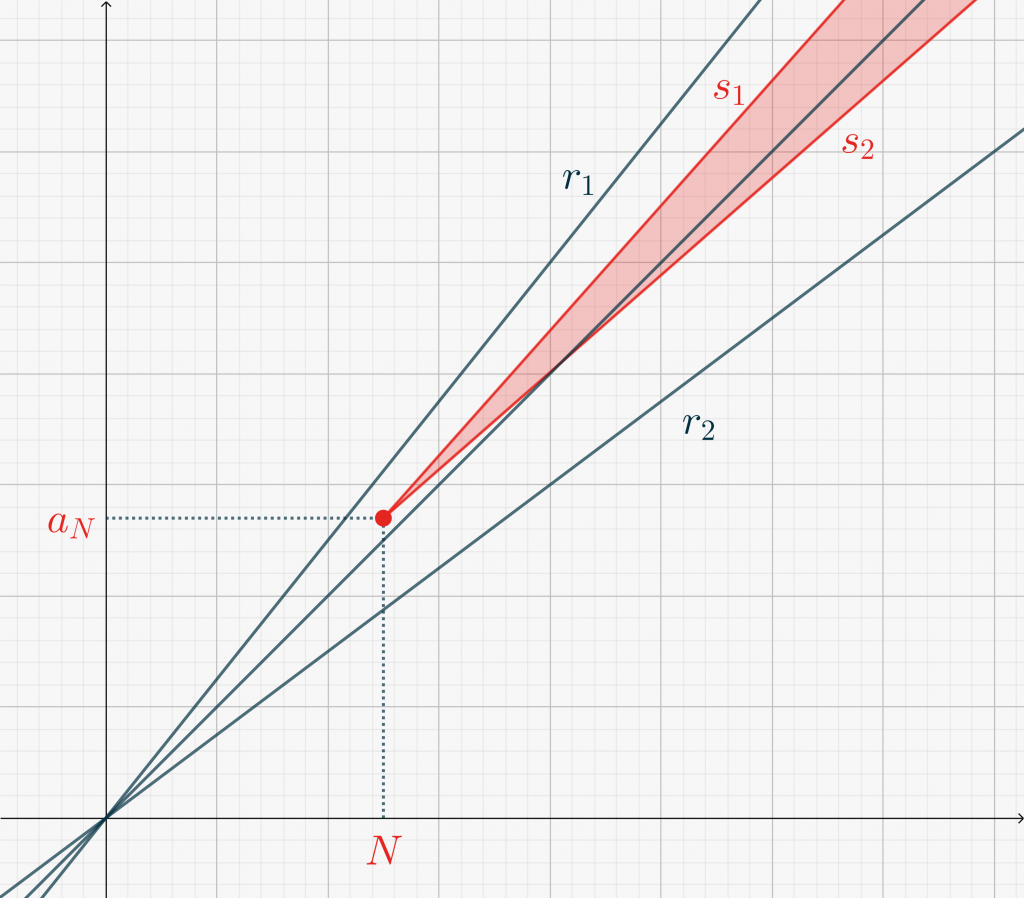
If \(P_N\) lies above \(r_1\), then we must find the intersection between \(r_1\) and \(s_1\). This leads to \[N_\varepsilon = \left\lceil \frac{2}{\varepsilon}(a_N – N)-N\right\rceil.\]This situation is depicted in the following Figure.
Similarly, if \(P_N\) lies below \(r_2\) we need to find the intersection between \(r_2\) and \(s_2\), leading to \[N_\varepsilon = \left\lceil \frac{2}{\varepsilon}(N -a_N)-N\right\rceil.\]
In conclusion, once \(N\) has been chosen according to condition \eqref{eq3531:3}, selecting \[N_\varepsilon = \max\left\{N, \left\lceil \frac{2}{\varepsilon}(a_N – N)-N\right\rceil, \left\lceil \frac{2}{\varepsilon}(N – a_N)-N\right\rceil\right\}\]guarantees \eqref{eq3531:2}, and the thesis follows.
(Putnam 2006, Exercise B.6). Let \(k\) be an integer greater than \(1\). Suppose \(a_0 > 0\), and define \[a_{n+1} = a_n + \frac{1}{\sqrt[k]{a_n}}\]for \(n > 0\). Evaluate \[\lim_{n \to \infty} \frac{a_n^{k+1}}{n^k}.\]
- The sequence \((a_n)\) is monotonically increasing, therefore it must have a limit, either finite or infinite. If \(\lim_{n\to\infty} a_n = a<\infty\), then \((a_{n+1}-a_n)\) is a null sequence. Show that this generates a contradiction. Thus the sequence diverges.
- Let \(b_n = a_n^{\frac{k+1}k}\). (Note that \(b_n\), too, is divergent.) Using the fundamental limit \[\frac{(1+\alpha)^m-1}{\alpha} \to m\] when \(\alpha \to 0\), show that \[b_n-b_{n-1} \to \frac{k+1}k\] when \(n\to \infty\).
- Use this result, and the Theorem we just proved, to show that, for \(n\to \infty\), \[\frac{b_n}{n\cdot\frac{k+1}k} \to 1.\]
- Conclude that \[\lim_{n \to \infty} \frac{a_n^{k+1}}{n^k} = \left(\frac{k+1}k\right)^k.\]
