Nel risolvere un esercizio per i miei allievi, mi sono imbattuto nel seguente sotto-problema: data una successione divergente \(a_n\) tale per cui \(\lim_{n\to \infty} (a_{n+1}-a_n) = 1\), possiamo dire che \((a_n) \sim n\)? La risposta, nella forma che vi propongo, richiede qualche disegno e mi pare un utile modo per prendere dimestichezza con la definizione di limite.
Teorema. Sia \((a_n\)) una successione divergente tale per cui \[\lim_{n\to +\infty} (a_{n+1}-a_n) = 1,\tag{1}\label{eq3574:1}\] allora si ha \[\lim_{n\to +\infty} \frac{a_n}{n} = 1.\]
Per ogni \(\varepsilon > 0\), dobbiamo trovare un \(N_\varepsilon>0\) tale per cui, per ogni \(n> N_\varepsilon\), \[\left|\frac{a_n}{n}-1\right|<\varepsilon\tag{2}\label{eq3574:2}.\]
Osserva che la condizione \eqref{eq3574:2} è equivalente ad affermare che, per \(n\) sufficientemente grande, i punti \(P_n(n,a_n)\) devono trovarsi tra le rette \(r_1\) e \(r_2\) di equazioni \(y=(1+\varepsilon) x\) e \(y=(1-\varepsilon) x\) rispettivamente. Chiamiamo per semplicità questa regione del piano cartesiano \(\mathcal Q_\varepsilon\).
Grazie a \eqref{eq3574:1}, possiamo affermare che esiste un \(N\) tale che, per \(k\geq N\), \[a_k+1-\frac{\varepsilon}2 < a_{k+1}< a_k+1+\frac{\varepsilon}2.\tag{3}\label{eq3574:3}\]
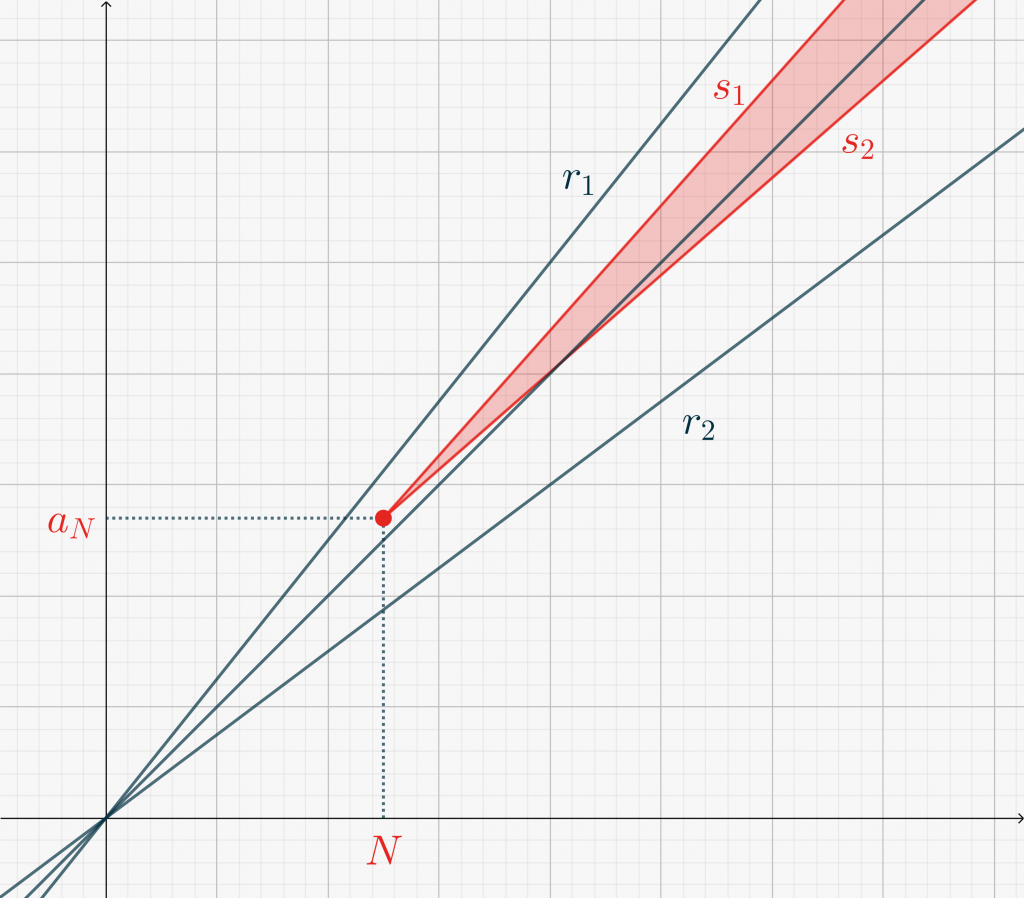
Applicando ripetutamente \eqref{eq3574:3} per \(k=N,N+1,\dots,N+n\), si ricava\[a_N + n – n\frac{\varepsilon}2< a_{N+n} < a_N + n + n\frac{\varepsilon}2,\tag{4}\label{eq3574:4}\] valida per ogni \(n>0\). Nuovamente, è utile interpretare \eqref{eq3574:4} geometricamente. Questa equazione ci dice che per \(n>0\) i punti \(P_{N+n}(N+n,a_{N+n})\) sono contenuti nella regione compresa tra le rette \[s_1 : \ \ y=(x-N)\left(1+\frac{\varepsilon}2\right) + a_N\] e\[s_2 : \ \ y=(x-N)\left(1-\frac{\varepsilon}2\right) + a_N\](la regione corrisponde all’area ombreggiata nelle figure qui sotto).
La pendenza di queste rette è stata scelta in modo tale che, se \(P_N \in \mathcal Q_\varepsilon\), anche i punti \(P_n\) per \(n>N\) si trovano in \(\mathcal Q_\varepsilon\). Questo ci permette di scegliere, in questo caso \(N_\varepsilon = N\). Vedi Figura qui sotto. Osserva che in questo scenario le intersezioni delle le rette \(r_1\) e \(r_2\) con \(s_1\) e \(s_2\) si trovano tutti in corrispondenza di un’ascissa \(x < N\).
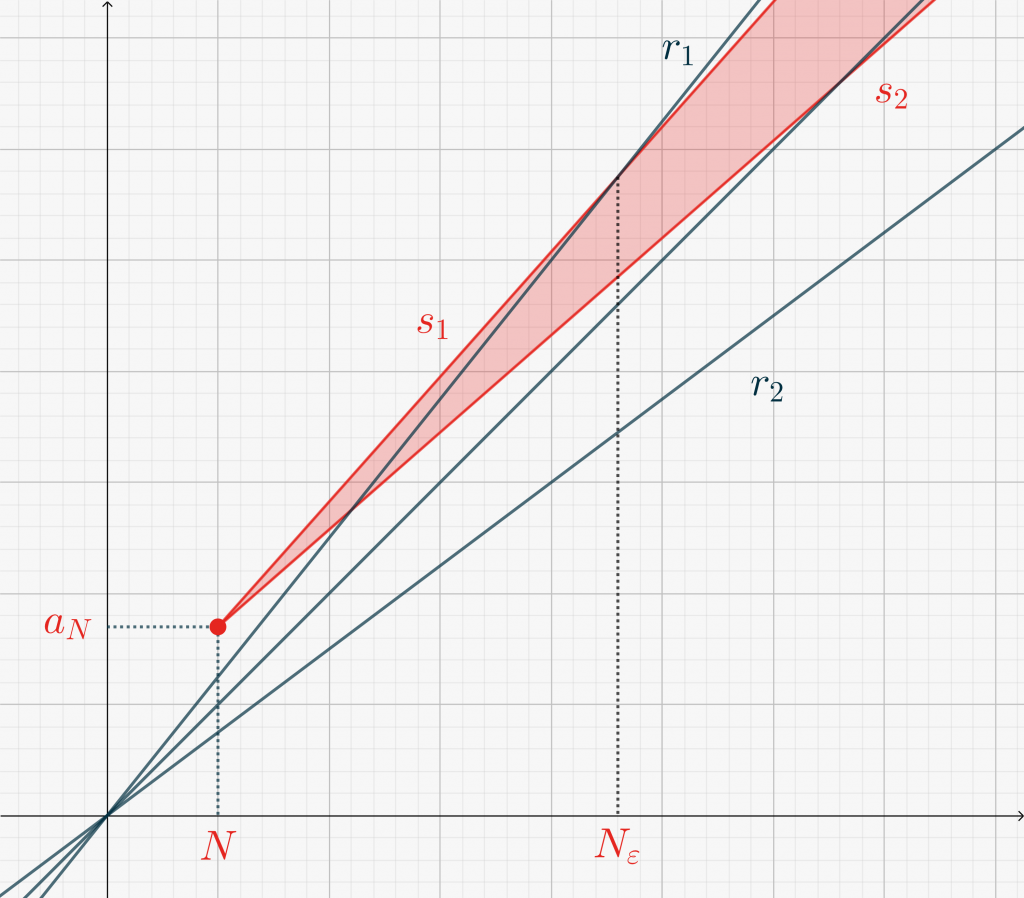
Se invece \(P_N\) giace al di sopra di \(r_1\), allora dobbiamo trovare l’ascissa dell’intersezione tra \(r_1\) e \(s_1\). Questo ci porta ad avere \[N_\varepsilon = \left\lceil \frac{2}{\varepsilon}(a_N – N)-N\right\rceil.\]La situazione è rappresentata nella Figura seguente.
Analogamente, se \(P_N\) giace sotto \(r_2\), \(N_\varepsilon\) si trova intersecando \(r_2\) e \(s_2\); otteniamo allora \[N_\varepsilon = \left\lceil \frac{2}{\varepsilon}(N -a_N)-N\right\rceil.\]
In conclusione, una volta che \(N\) è stato scelto basandosi sulla condizione \eqref{eq3574:3}, selezionando \[N_\varepsilon = \max\left\{N, \left\lceil \frac{2}{\varepsilon}(a_N – N)-N\right\rceil, \left\lceil \frac{2}{\varepsilon}(N – a_N)-N\right\rceil\right\}\]abbiamo la garanzia che \eqref{eq3574:2} sia soddisfatta, da cui la tesi.
(Putnam 2006, Esercizio B.6). Sia \(k\) un intero maggiore di \(1\). Dato \(a_0 > 0\), definisci ricorsivamente \[a_{n+1} = a_n + \frac{1}{\sqrt[k]{a_n}}\]per \(n > 0\). Determina\[\lim_{n \to \infty} \frac{a_n^{k+1}}{n^k}.\]
- La successione \((a_n)\) è monotona crescente, quindi ammette limite, finito o infinito. Se \(\lim_{n\to\infty}a_n = a < \infty\) allora la successione \((a_{n+1}-a_n)\) è infinitesima. Mostra che ciò porta a una contraddizione. Deduci che \((a_n)\) diverge.
- Sia \(b_n = a_n^{\frac{k+1}k}\). Osserva che anche \(b_n\) diverge. Usando il limite notevole\[\frac{(1+\alpha)^m-1}{\alpha} \to m\]per \(\alpha \to 0\), mostra che \[b_n-b_{n-1} \to \frac{k+1}k\] quando \(n\to \infty\).
- Usa questo risultato e il Teorema appena dimostrato per verificare che, per \(n\to \infty\), \[\frac{b_n}{n\cdot\frac{k+1}k} \to 1.\]
- Concludi che \[\lim_{n \to \infty} \frac{a_n^{k+1}}{n^k} = \left(\frac{k+1}k\right)^k.\]
