Se i grafici di due funzioni reali \(f\) and \(g\) si “incrociano” esisterà almeno un punto di intersezione tale per cui \(f(x) = g(x)\). Questa è una conseguenza del teorema dei valori intermedi. La presenza di una intersezione non è però garantita se una delle due funzioni non è continua.
Traiamo ancora ispirazione da una funzione che è stata descritta in un post precedente. Ricordiamo brevemente ch \(f: [0, +\infty) \to [0, + \infty)\) mappa il numero reale \(x\) con rappresentazione decimale \[x = \sum_k a_k 10^k,\] in\[f(x) = \sum_{k} a_{2k}10^k,\] mantenendo quindi solo le cifre di \(x\) che originariamente occupavano posizioni pari. In caso di ambiguità nella notazione, utilizziamo la versione decimale finita (quindi ad esempio useremo \(1\), invece di \(0.999\dots\)). `E stato mostrato nei post precedenti che \(f\) è discontinua in un sottoinsieme denso del suo dominio, pur essendo continua quasi ovunque (in particulare in tutti i numeri con rappresentazione decimale infinita).
Supponiamo che una funzione continua \(g\) attraversi uno dei tratti rettilinei che approssimano \(f\) (vedi figura qui sotto). Possiamo affermare che esista un punto \(a\) tale per cui \(f(a) = g(a)\)? Per essere sicuri che ciò accada, abbiamo bisogno, da parte di \(g\), di una condizione più forte della continuità.
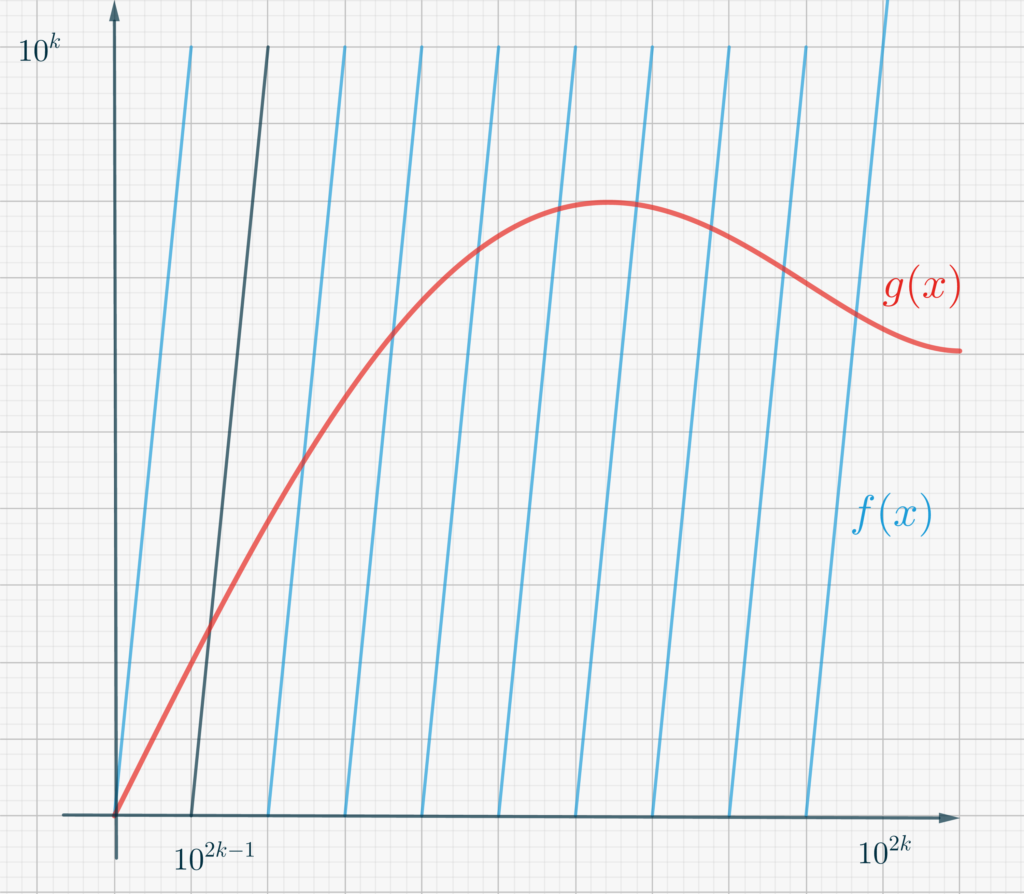
Abbiamo bisogno che la funzione sia lipschitziana in un intervallo in cui i due grafici si attraversano. Si dice che \(g\) è lipschitziana in un intervallo \([a, b]\) se esiste un numero \(M\) tale che, per ogni \(x\) e \(y\) in \([a,b]\), \[|g(x)-g(y)| \leq M |x-y|\tag{1}\label{eq3451:1}.\] Ovviamente se \(g \in C^1\), ovvero se \(g\) ha derivata prima continua, allora la condizione \eqref{eq3451:1} è soddisfatta.
Dimostreremo quanto segue.
Teorema. Data la funzione \(f\) definita più sopra e una funzione \(g\) che sia lipschitziana in \([0, b]\), con \(g(0) = 0\), esiste un punto \(a \in (0,b]\) tale per cui \[f(a) = g(a).\]
La dimostrazione del teorema si basa sulla costruzione una procedure che termine quando \(a\) è stato trovato, oppure genera una successione \((a_n)\) che converge al punto cercato.
- In primo luogo dobbiamo determinare il corretto “fattore di scala”. A questo scopo scegliamo \(k\) in modo tale che \[10^k< \min\left\{\frac{20}M,\ \ \sqrt b\right\},\]dove \(M\) è la quantità che garantisce la condizione \eqref{eq3451:1}. Mostra che con questa scelta \(g\) è lipschitziana in \(\left[0, 10^{2k}\right]\) è che il grafico di \(g\) necessariamente attraversa il secondo segmento rettilineo da sinistra in Figura 1 (quello in blu scuro).
- La prima “approssimazione” di \(a\) che otteniamo è \(a_0\), il punto di intersezione tra questa linea retta e \(g(x)\), la cui esistenza è garantita dal teorema dei valori intermedi. Verifica che \(a_0\) è soluzione dell’equazione \[g(x) = 10^{-k+1}\left(x-10^{2k-1}\right).\] Ora possiamo effettuare uno “zoom” sulla linea, il che ci mostra la situazione rappresentata in Figura 2.
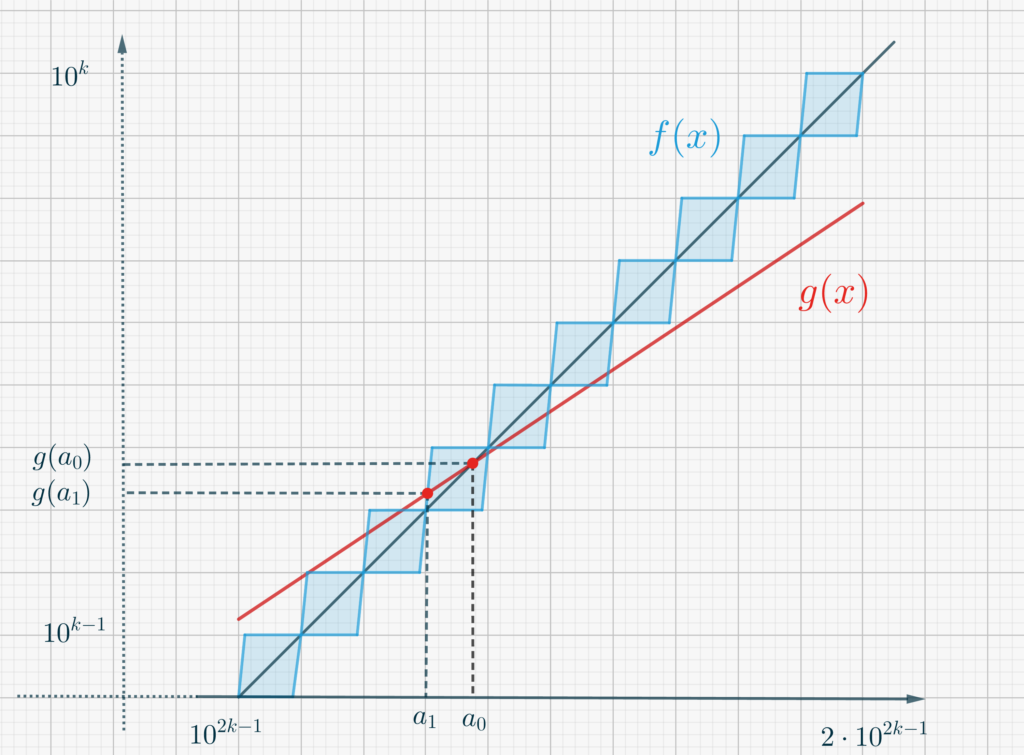
- Ricorda che \(f\) è confinata nei parallelogrammi ombreggiati in Figura (che opportunamente ingranditi sono repliche di quanto mostrato in Figura 1). Mostra che o \(\left(a_0, g(a_0)\right)\) è il vertice di uno di questi parallelogrammi oppure \(g(x)\) interseca il lato destro o sinistro del parallelogramma in cui è contenuta l’intersezione (fai uso della condizione di lipschitzianità di \(g\)!). Il primo caso si verifica se la cifra meno significativa di \(a_0\) è quella in posizione \((k-1)\); allora \(a=a_0\), terminando così la ricerca del punto di intersezione. Nel secondo caso, osserva che \[|f(a_0) – g(a_0)| \leq 10^{k-1},\] e che possiamo raffinare la stima di \(a\) cercando il punto di intersezione tra \(g\) e uno dei lati tra il destro e il sinistra del parallelogramma in questione.
- Trova l’equazione dei lati destro e sinistro del parallelogramma contenente il punto di coordinate \(\left(a_0, g(a_0)\right)\). Concludi che una migliore stima di \(a\), ovvero \(a_1\), è una soluzione dell’equazione \[g(x) =10^{-k+2}\left(x – \frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}\right) + f\left(\frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}\right),\] purché sia \( \frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}<a_1<\frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+10^{2k-3}\), oppure una soluzione di \begin{eqnarray}g(x) &=&10^{-k+2}\left(x – \frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+9\cdot 10^{2k-3}\right) + \\ & &+f\left(\frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+9\cdot 10^{2k-3}\right),\end{eqnarray} con \( \frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+9\cdot 10^{2k-3}<a_1<\frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+10^{2k-2}\), dove \([\cdot]\) rappresenta la parte intera della quantità in parentesi quadre.
- Dimostra che se la procedura non termina a un numero con rappresentazione decimale finita, allora, a ogni passo \(n=2,3,\dots\) dovremo determinare \(a_n\) come soluzione di \[g(x) = 10^{-k+n+1}\left(x – \frac{\left[10^{-2k+2n}a_{n-1}\right]}{10^{-2k+2n}}\right) + f\left(\frac{\left[10^{-2k+2n}a_{n-1}\right]}{10^{-2k+2n}}\right)\] oppure di \begin{eqnarray}g(x) &=& 10^{-k+n+1}\left(x – \frac{\left[10^{-2k+2n}a_{n-1}\right]}{10^{-2k+2n}}+9\cdot 10^{2k-2n-1}\right) +\\ & &+ f\left(\frac{\left[10^{-2k+2n}a_{n-1}\right]}{10^{-2k+2n}}+9\cdot 10^{2k-2n-1}\right).\end{eqnarray}
- Verifica che \[|f(a_n) – g(a_n)| \leq 10^{k-n},\tag{2}\label{eq3451:2}\] e che per ogni \(m,\ n \geq 0\),\[|a_{n+m}-a_n|\leq 10^{k-2n-1}\tag{3}\label{eq3451:3}.\]
- Puoi affermare, usando la condizione \eqref{eq3451:3}, che \((a_n)\) è una successione di Cauchy? Questo implica che essa converge a un punto \(a\). Nota che la rappresentazione di \(a\) è necessariamente infinita.
- Usa la continuità di \(f\) e \(g\) in \(a\) per concludere che le successioni \(\left(f(a_n)\right)\) e \(\left(g(a_n)\right)\) convergono rispettivamente a \(f(a)\) e \(g(a)\).
- Infine, da \eqref{eq3451:2}, deduci che \[f(a) = g(a),\]come richiesto.
Se \(g\) è continua ma non lipschitziana, non possiamo trarre alcuna conclusione riguardo all’esistenza di punti di intersezione con \(f\).
- Considera ad esempio la funzione \[g(x) = \sqrt x.\] Osserva che \[g\left(25\cdot 10^{2k}\right) = 5 \cdot 10^k = f\left(25\cdot 10^{2k}\right), \forall \ k \in \Bbb Z.\]
- Mostra che il più piccolo numero \(x_k\) per cui vale \(f(x_k) = 10^k\) è \[x_k = \frac{10^{2k}}{11} = \sum_{h=1}^{+\infty} 9\cdot 10^{2k- 2h}.\]Considera quindi i punti \(A_k(x_k,f(x_k))\) e concludi che la spezzata che passa per gli \(A_k\), i.e. \[g(x) = \begin{cases} 0 & (x=0)\\ 10^{-k}\left(x-\frac{10^{2k}}{11}\right) + 10^k & \frac{10^{2k}}{11}<x\leq \frac{10^{2k+2}}{11}, \ \forall k\in \Bbb Z\end{cases}\] è tale per cui \(g(x)\geq f(x)\), con l’uguaglianza solo per \(x= 0\) e per \(x=x_k\), \(k\in\Bbb Z\).
- Considera la funzione concava \[g(x) = \sqrt{11 x}.\] Osserva che \(g\) passa per i punti \(A_k\). Concludi che qualunque funzione \[h(x) = K\sqrt x,\] con \(K>\sqrt{11}\), non ha con \(f\) alcuna intersezione tranne \(x=0\), pur essendo continua in \([0, +\infty)\) e differenziabile in \((0, +\infty)\).
