Raramente abbiamo necessità di ricorrere alla definizione di integrale. La maggior parte delle volte, infatti, si ha a che fare con funzioni molto “regolari” per le quali sono disponibili una serie di trucchi e regole per svolgere il calcolo. In questo post diamo un esempio di una situazione in cui l’uso della definizione è strettamente necessario.
Consideriamo ancora la funzione presentata nel post precedente, come esercizio: si tratta della funzione \(f\) that conserva soltanto le cifre pari della rappresentazione decimale del suo ingresso. Quindi, se \[x = \sum_k a_k 10^k,\] con \(k\in \Bbb Z\) e \(a_k \in\{ 0,1,\dots,9\}\), allora \[f(x) = \sum_k a_{2k} 10^k.\]Per esempio \[f(59842.1073) = 582.03.\]
In quel post abbiamo elencato alcune interessanti caratteristiche di questa funzione. Qui vogliamo dimostrare, usando soltanto la definizione, che \(f\) è integrabile secondo Riemann. Calcoleremo anche il valore di \[\int_0^{10^{2k}} f(x) dx, \ \ k\in\Bbb Z.\]
In primo luogo, osserva che la funzione è auto-simile. Infatti \[f\left(10^{2k}x\right) = 10^k f(x),\tag{1}\label{eq3367:1}\] per ogni \(k \in \Bbb Z\). Se rappresentiamo il grafico della funzione in \(\left[0, 10^{2k}\right]\times \left[0,10^k\right]\) otteniamo sempre la forma mostrata in Figura qui sotto.
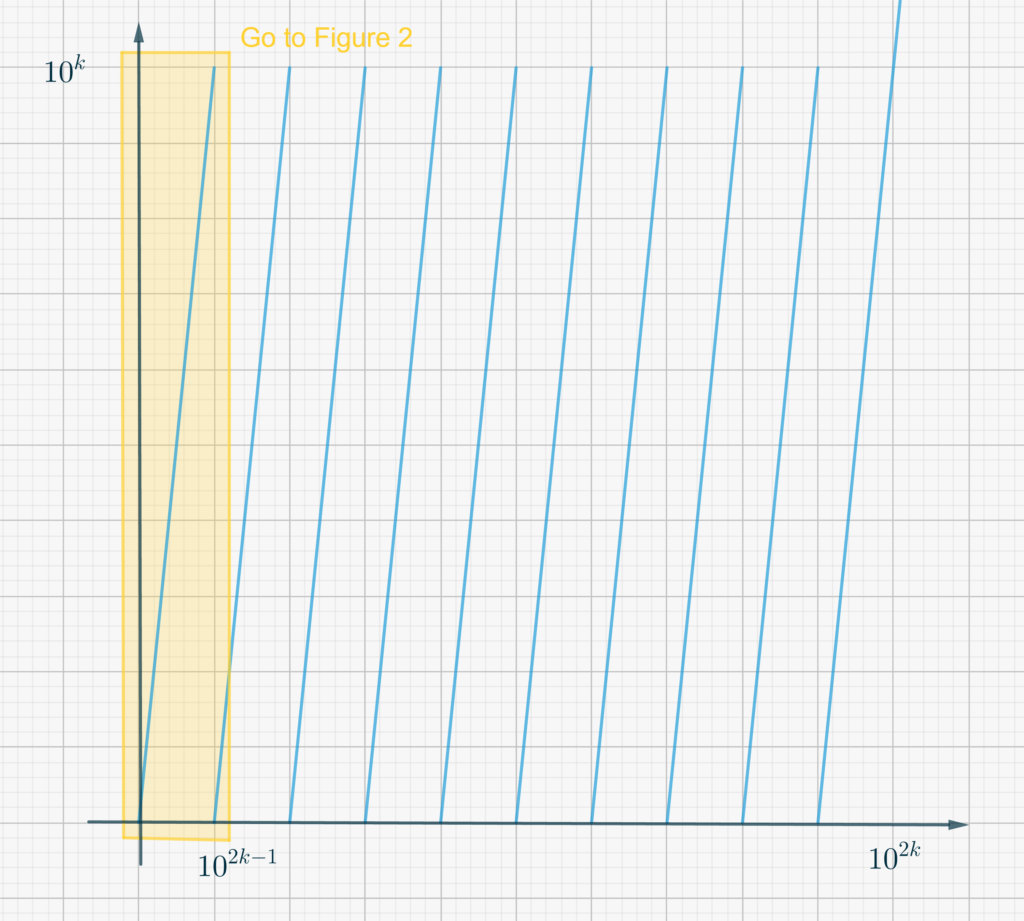
Ingrandendo l’area colorata otteniamo il grafico che segue.
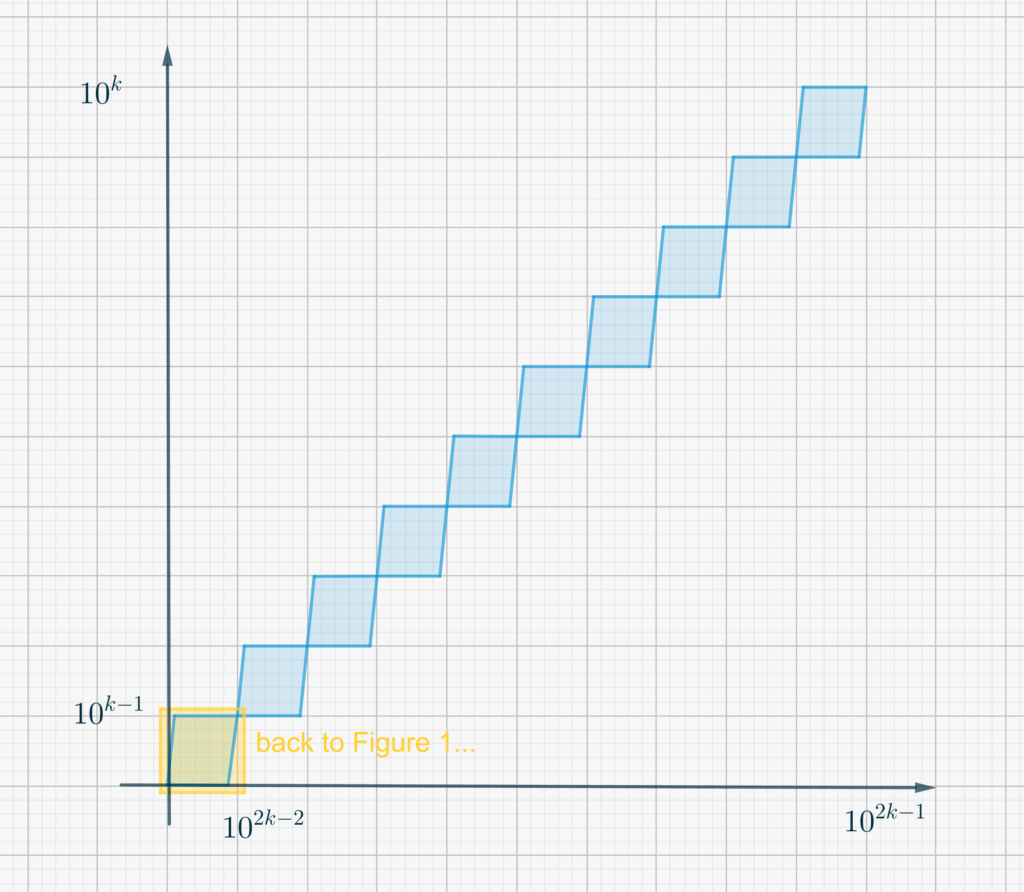
In Figura 2, the function è confinata all’interno dell’area tratteggiata azzurra. Se ingrandiamo ancora la zona gialla, ritorniamo a una copia esatta di quanto mostrato in Figura 1, sebbene nel nuovo “range” \(\left[0,10^{2k-2}\right]\times \left[0,10^{k-1}\right]\), in accordo con l’espressione \eqref{eq3367:1}.
Prima di procedere, ricorda che una funzione limitata \(f\) è integrabile nell’intervallo \([a,b]\) se l’integrale inferiore e superiore su quell’intervallo coincidono. A loro volta, questi sono definiti rispettivamente come l’estremo superiore delle somme inferiori e l’estremo inferiore delle somme superiori, dove gli estremi sono presi su tutte le possibili partizioni dell’intervallo \([a,b]\).
- Considera la somma superiore di \(f\) nell’intervallo \(\left[0,10^{2k}\right]\) con la partizione \(\left(0,10^{2k-1},2\cdot 10^{2k-1},\dots, 9\cdot 10^{2k-1},10^{2k}\right)\) e mostra, con l’aiuto di Figura 1, che essa è uguale a \(\frac12\cdot 10^{3k}\).
- Cerchiamo ora di costruire una successione di somme inferiori che converge a \(\frac12\cdot 10^{3k}\), sfruttando la struttura “annidata” di \(f\). Allo scopo, sia \(\mathcal L^{(k)}_n\) la somma inferiore di \(f\) sull’intervallo \[\left[0,10^{2k}\right],\] con partizione \[\left(0,10^{2k-2n},2\cdot 10^{2k-2n},\dots, 10^{2n-1}\cdot 10^{2k-2n},10^{2k}\right),\]in cui l’intervallo è stato diviso in \(10^{2n}\) sotto-intervalli di uguale ampiezza.
- Mostra che \(\mathcal L^{(k)}_0 = 0\). Questo risultato si ottiene con la partizione “banale” costituita da un unico sotto-intervallo.
- Ora incrementa il numero di sotto-intervalli a \(100\). Osserva la Figura 2 ed in particolare nota che la somma delle aree di tutti i rettangoli di lato \(10^{2k-2}\times 10^{k-1}\) sotto il grafico della \(f\) è pari \(45 \cdot 10^{3k-3}\). Dato che nell’intervallo \(\left[0,10^{2k}\right]\) ci sono \(10\) repliche di questo grafico (osserva anche la Figura 1), puoi concludere che \[\mathcal L^{(k)}_1 = 45 \cdot 10^{3k-2}.\]
- Per ottenere una somma inferiore più elevata, occorre aumentare il numero di sotto-intervalli di un altro fattore \(100\). Guarda ancora la Figura 2 and quindi la Figura 1: dobbiamo aggiungere a \(\mathcal L^{(k)}_1\) cento repliche di \(\mathcal L^{(k-1)}_1\). Quindi si ottiene \begin{eqnarray}\mathcal L^{(k)}_2 &=& 45\cdot 10^{3k-2} + 10^2\cdot\mathcal L^{(k-1)}_1=\\ &=&45 \cdot \left(10^{3k-2}+10^{3k-3}\right).\end{eqnarray}
- Iterando quanto fatto nel punto 5., dimostra che, per \(n \geq 1\), \[\mathcal L^{(k)}_n = 45\cdot 10^{3k-2} \cdot \sum_{h=0}^{n-1}10^{-h}.\]
- Dimostra che la sequenza \(\left(\mathcal L^{(k)}_n\right)\) converge a \(\frac12 \cdot 10^{3k}\). Spiega perché, considerando anche quanto mostrato nel punto 1., possiamo concludere che \(f\) è integrabile secondo Riemann e che\[\int_0^{10^{2k}} f(x) dx = \frac12 \cdot 10^{3k}.\]