Very seldom does one need to make use of the actual definition of Riemann integral. Most of the times, in fact, we are dealing with very “regular” functions for which a whole bunch of tricks and rules are available. We offer here an example where resorting to the definition is necessary.
Let us consider again the function proposed in the previous post, as an exercise: it is the function \(f\) that preserves only the even digits of its input. So, if \[x = \sum_k a_k 10^k,\] with \(k\) possibily ranging over all integers and \(a_k \in\{ 0,1,\dots,9\}\), then \[f(x) = \sum_k a_{2k} 10^k.\]For example \[f(59842.1073) = 582.03.\]
In that post we pointed out some interesting properties of the function. Here we want to show, merely by definition, that \(f\) is Riemann integrable. We will also calculate the exact value of \[\int_0^{10^{2k}} f(x) dx, \ \ k\in\Bbb Z.\]
As a first step, notice that the function is self-similar. In fact \[f\left(10^{2k}x\right) = 10^k f(x),\tag{1}\label{eq3303:1}\] for any \(k \in \Bbb Z\). If we plot the function in the range \(\left[0, 10^{2k}\right]\times \left[0,10^k\right]\) we always see the shape shown in the Figure below.
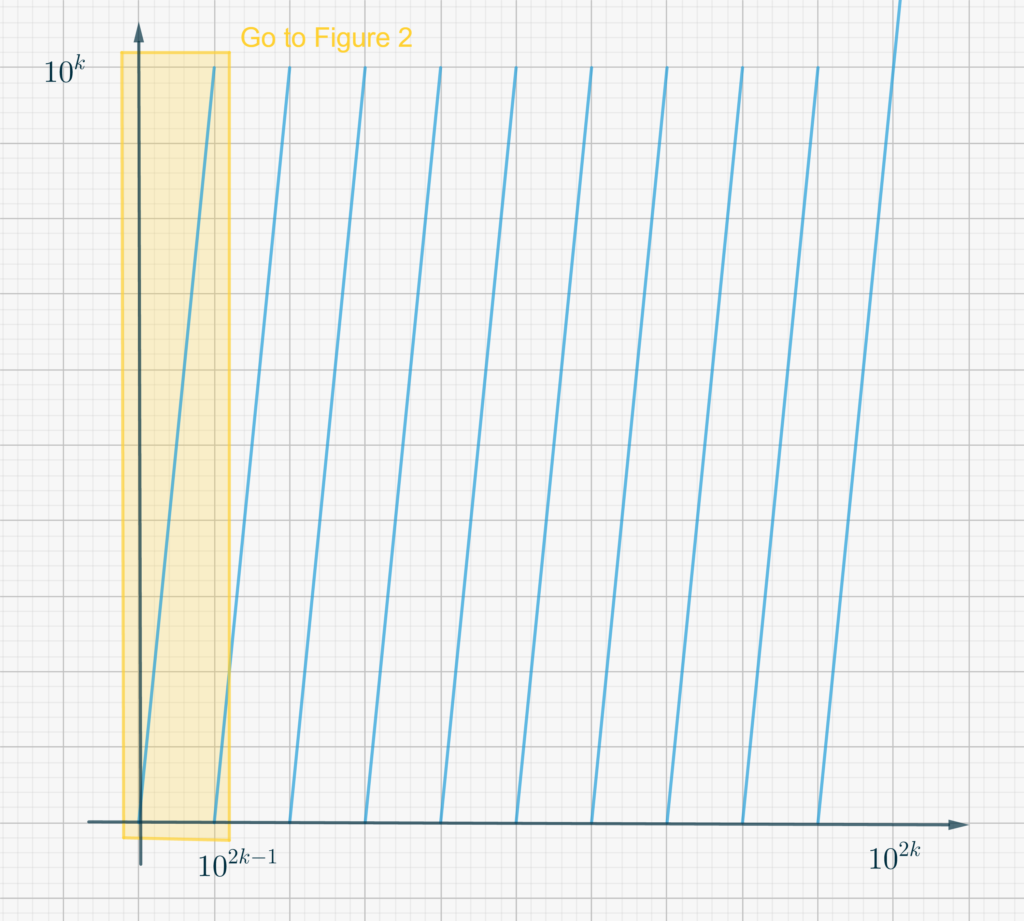
Magnifying the shaded area, leads to something like this:
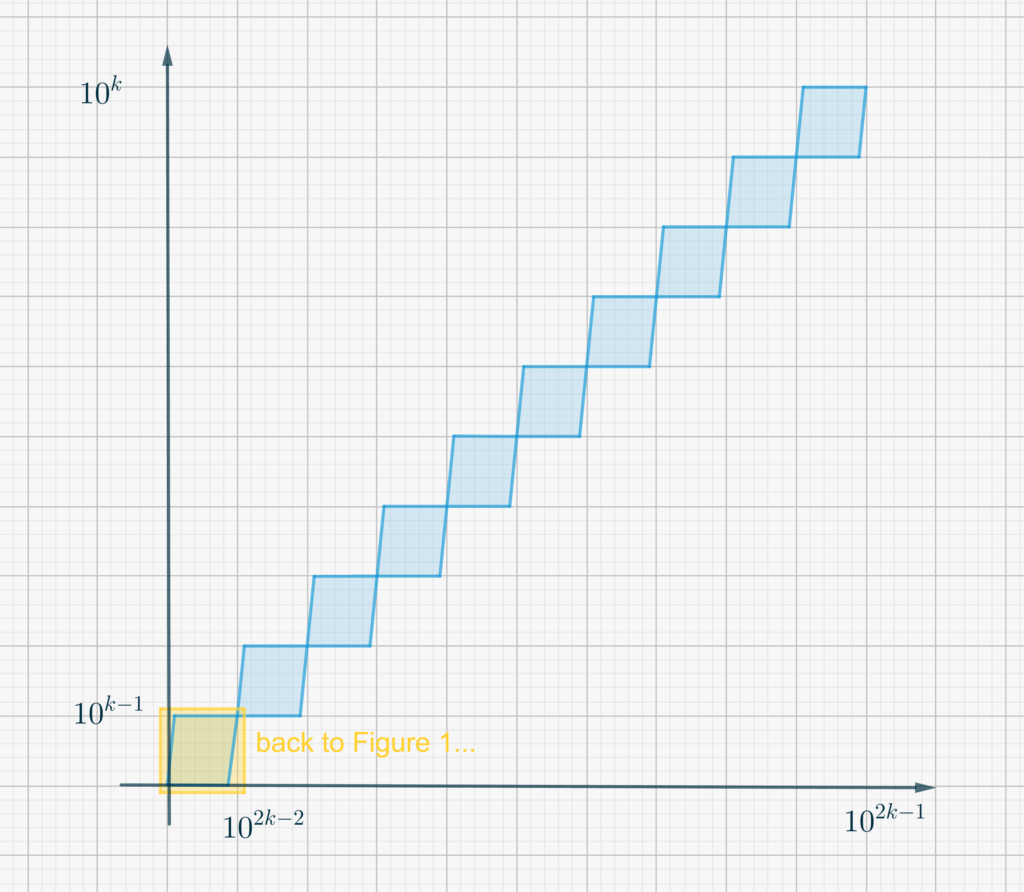
In Figure 2, the function is confined within the light blue shaded area. If we further zoom in the yellow area, we get back to an exact copy of what is shown in Figure 1, although in the new range \(\left[0,10^{2k-2}\right]\times \left[0,10^{k-1}\right]\), in accordance with \eqref{eq3303:1}.
Before proceeding, recall that a bounded function \(f\) is integrable over an interval \([a,b]\) if the lower and upper integrals over that interval coincide. Those are, in turn, defined as the supremum of the lower sums, and the infimum of the upper sums, respectively, where inf and sup are taken over all possible partitions of the interval \([a,b]\).
- Consider the upper sum of the function \(f\) in the interval \(\left[0,10^{2k}\right]\) with partition \(\left(0,10^{2k-1},2\cdot 10^{2k-1},\dots, 9\cdot 10^{2k-1},10^{2k}\right)\), and show, with the help of Figure 1, that it is equal to \(\frac12\cdot 10^{3k}\).
- We now aim at constructing a sequence of lower sums that converges to \(\frac12\cdot 10^{3k}\), by taking advantage of the nested structure of \(f\). To this aim, let \(\mathcal L^{(k)}_n\) be the lower sum of \(f\) over the interval \[\left[0,10^{2k}\right],\] with partition \[\left(0,10^{2k-2n},2\cdot 10^{2k-2n},\dots, 10^{2n-1}\cdot 10^{2k-2n},10^{2k}\right),\]in which the interval has been divided into \(10^{2n}\) equal sized sub-intervals.
- Show that \(\mathcal L^{(k)}_0 = 0\). This is obtained with the trivial partition with no subintervals.
- Now increase the number of sub-intervals to \(100\). Observe Figure 2 and notice that the sum of all rectangles of sides \(10^{2k-2}\times 10^{k-1}\) below the graph of \(f\) have overall area \(45 \cdot 10^{3k-3}\). Since in the range \(\left[0,10^{2k}\right]\) we have \(10\) replicas of this shape (see also Figure 1), conclude that \[\mathcal L^{(k)}_1 = 45 \cdot 10^{3k-2}.\]
- In order to get a higher lower sum, we must increase the number of sub-intervals by another factor \(100\). Look again at Figure 2 and then Figure 1, and notice that this computation involves adding to \(\mathcal L^{(k)}_1\) one hundred replicas of \(\mathcal L^{(k-1)}_1\). So we have \begin{eqnarray}\mathcal L^{(k)}_2 &=& 45\cdot 10^{3k-2} + 10^2\cdot\mathcal L^{(k-1)}_1=\\ &=&45 \cdot \left(10^{3k-2}+10^{3k-3}\right).\end{eqnarray}
- By further iteration of the procedure shown in 5. demonstrate that for \(n \geq 1\) \[\mathcal L^{(k)}_n = 45\cdot 10^{3k-2} \cdot \sum_{h=0}^{n-1}10^{-h}.\]
- Show, that the sequence \(\left(\mathcal L^{(k)}_n\right)\) converges to \(\frac12 \cdot 10^{3k}\). Explain why this conclusion, together with point 1., demonstrates that \(f\) is Riemann integrable and that\[\int_0^{10^{2k}} f(x) dx = \frac12 \cdot 10^{3k}.\]
