If the graphs of two continuous real functions \(f\) and \(g\) “cross” each other, then there must be at least an intersection point for which \(f(x) = g(x)\). This is a consequence of the Intermediate Value Theorem. But intersections are no longer guaranteed if one of the two functions is not continuous.
We draw again inspiration from a function we learned to know in an older post. We briefly recall here that \(f: [0, +\infty) \to [0, + \infty)\) maps the point \(x\) with decimal expansion \[x = \sum_k a_k 10^k,\] into \[f(x) = \sum_{k} a_{2k}10^k,\] keeping thus only the enven positioned digits of the input number \(x\). In case of ambiguity in the notation, the finite version of the number is adopted (so we will use \(1\), rather than \(0.999\dots\)). We previously showed that \(f\) is discontinuous on a dense subset of its domain, despite being continuous almost everywhere (in particular at points with infinite decimal representation).
Suppose a continuous function \(g\) crosses one of the straight lines that approximate the behaviour of \(f\) (see the Figure below). Can we say that there is a point \(a\) such that \(f(a) = g(a)\)? In order to make sure this happens, we actually need – from \(g\)’s side – something stronger than continuity.
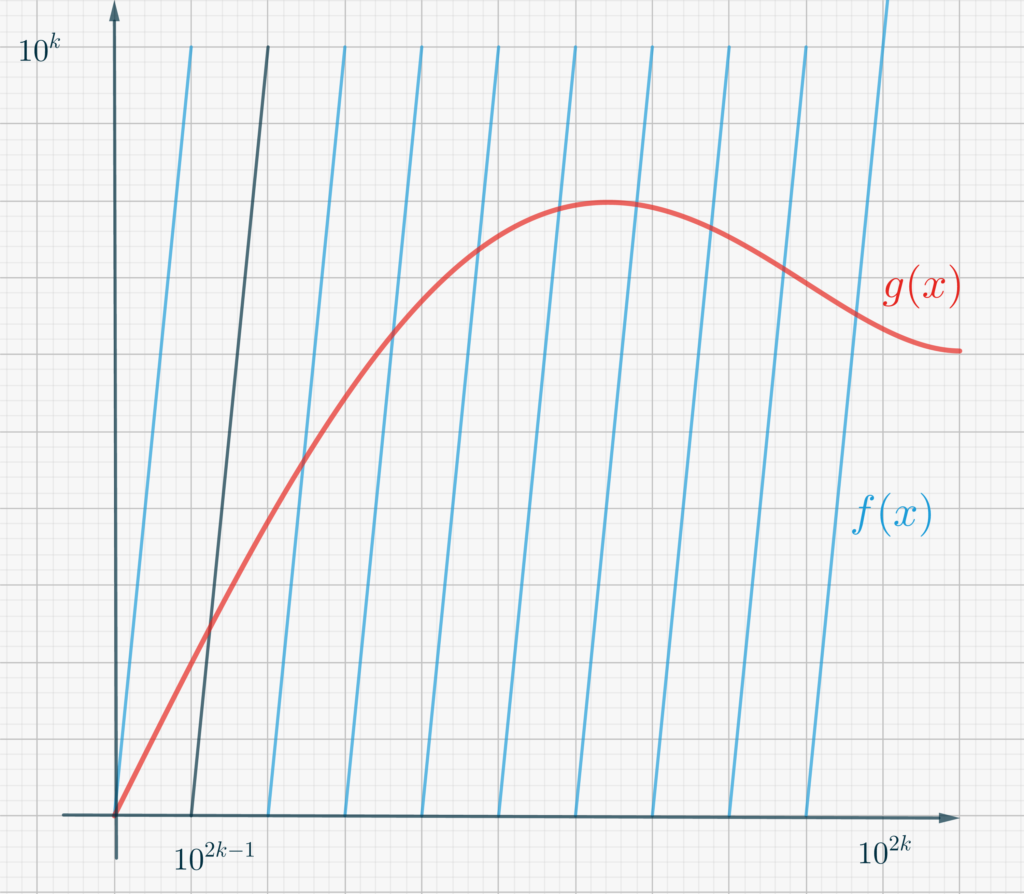
What we need is Lipschitz continuity, in an interval in which the two graphs cross. We say that \(g\) is Lipschitz continuous in an interval \([a, b]\) if there is an \(M\) such that, for all \(x\) and \(y\) in \([a,b]\), \[|g(x)-g(y)| \leq M |x-y|\tag{1}\label{eq3375:1}.\] Of course if \(g \in C^1\), that is if \(g\) is continuously differentiable, then condition \eqref{eq3375:1} certainly holds.
We will demonstrate the following.
Theorem. Given the function \(f\) defined above, and a function \(g\) that is Lipschitz continuous in \([0, b]\), with \(g(0) = 0\), then there exists a point \(a \in (0,b]\) such that \[f(a) = g(a).\]
In order to prove the Theorem we will devise a procedure that either stops when \(a\) is found or generates a sequence \((a_n)\) converging to the desired point.
- Firstly, we need to choose an appropriate “scale”. Thus we will choose \(k\) in such a way that \[10^k< \min\left\{\frac{20}M,\ \ \sqrt b\right\},\]where \(M\) is the number that guarantees \eqref{eq3375:1}. Show, then, that \(g\) is Lipschitz continuous in \(\left[0, 10^{2k}\right]\), and that the graph of \(g\) must cross the second straight line from the left in Figure 1 (the one marked in dark blue).
- Our first “approximation” to \(a\) is given by \(a_0\), the intersection point between this line and \(g(x)\), whose existence is guaranteed by the Intermediate Value Theorem. Show that \(a_0\) is a solution to the equation \[g(x) = 10^{-k+1}\left(x-10^{2k-1}\right).\] We can now zoom on the line and see what is shown below.
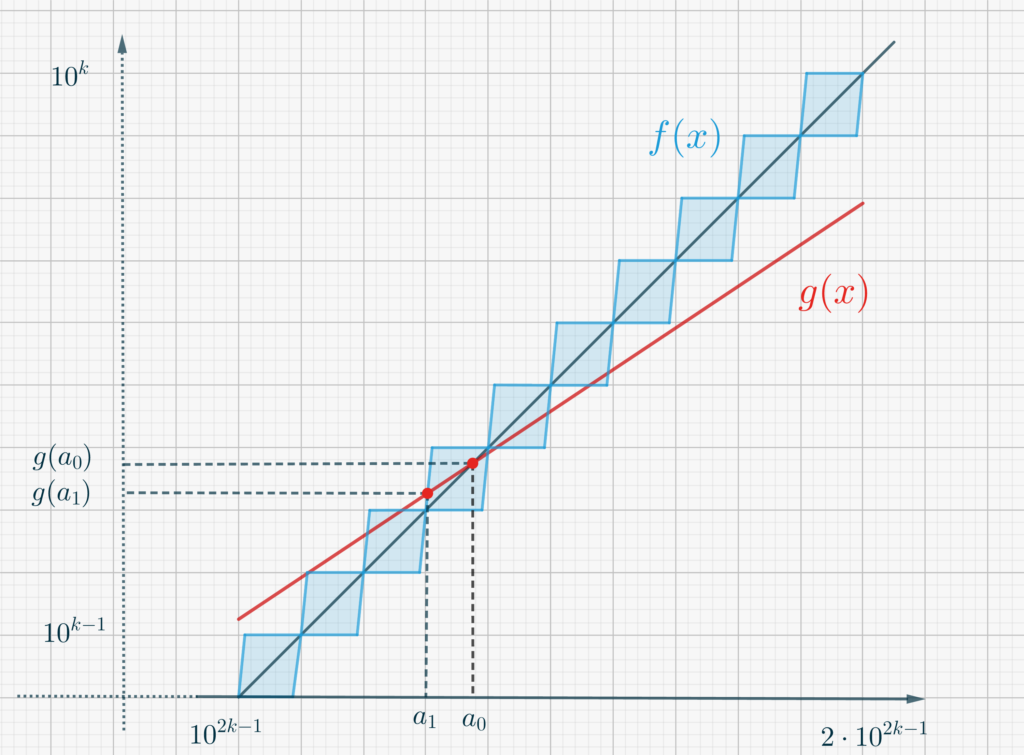
- Recall that \(f\) is confined within the dashed parallelograms (which, once magnified, are scaled replicas of Figure 1). Show that either the point \(\left(a_0, g(a_0)\right)\) is the vertex of one of such parallelograms, or \(g(x)\) intersects its left side or its right side (here, again, Lipschitz continuity comes into play!). In the first case, the least significant digit of \(a_0\) is the \((k-1)\)th one, and we can set \(a=a_0\), thus terminating the procedure. In the second case, however, we have \[|f(a_0) – g(a_0)| \leq 10^{k-1},\] and we can refine our approximation by finding the intersection between the graph of \(g\) and one of the “vertical” sides of the parallelogram.
- Find the equation of the left and right sides of the parallelogram containing \(\left(a_0, g(a_0)\right)\). Conclude that our refinement \(a_1\) is a solution to the equation \[g(x) =10^{-k+2}\left(x – \frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}\right) + f\left(\frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}\right),\] such that \( \frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}<a_1<\frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+10^{2k-3}\), or to the equation \begin{eqnarray}g(x) &=&10^{-k+2}\left(x – \frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+9\cdot 10^{2k-3}\right) + \\ & &+f\left(\frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+9\cdot 10^{2k-3}\right),\end{eqnarray} such that \( \frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+9\cdot 10^{2k-3}<a_1<\frac{\left[10^{-2k+2}a_0\right]}{10^{-2k+2}}+10^{2k-2}\), where \([\cdot]\) denotes the integral part of the number in brakets.
- Demonstrate that if the procedure does not stop to a terminating decimal number, then, at each step \(n=2,3,\dots\) you need to find the solution \(a_n\) to the equation \[g(x) = 10^{-k+n+1}\left(x – \frac{\left[10^{-2k+2n}a_{n-1}\right]}{10^{-2k+2n}}\right) + f\left(\frac{\left[10^{-2k+2n}a_{n-1}\right]}{10^{-2k+2n}}\right)\] or to the equation\begin{eqnarray}g(x) &=& 10^{-k+n+1}\left(x – \frac{\left[10^{-2k+2n}a_{n-1}\right]}{10^{-2k+2n}}+9\cdot 10^{2k-2n-1}\right) +\\ & &+ f\left(\frac{\left[10^{-2k+2n}a_{n-1}\right]}{10^{-2k+2n}}+9\cdot 10^{2k-2n-1}\right).\end{eqnarray}
- Show that \[|f(a_n) – g(a_n)| \leq 10^{k-n},\tag{2}\label{eq3375:2}\] and that, for \(m,\ n \geq 0\),\[|a_{n+m}-a_n|\leq 10^{k-2n-1}\tag{3}\label{eq3375:3}.\]
- Can you state, using \eqref{eq3375:3}, that \((a_n)\) is a Cauchy sequence? This implies that it converges to a non terminating decimal \(a\).
- Use continuity of \(f\) and \(g\) in \(a\) to conclude that the sequences \(\left(f(a_n)\right)\) and \(\left(g(a_n)\right)\) converge to \(f(a)\) and \(g(a)\) respectively.
- Finally, from \eqref{eq3375:2} deduce that \[f(a) = g(a),\]as desired.
If \(g\) is continuous but not Lipschitz, no conclusion can be drawn on the existence of strictly positive intersections with \(f\).
- Consider the function \[g(x) = \sqrt x,\] for example. Observe that \[g\left(25\cdot 10^{2k}\right) = 5 \cdot 10^k = f\left(25\cdot 10^{2k}\right), \forall \ k \in \Bbb Z.\]
- Show that the smallest point \(x_k\) for which \(f(x_k) = 10^k\) is \[x_k = \frac{10^{2k}}{11} = \sum_{h=1}^{+\infty} 9\cdot 10^{2k- 2h}.\]Consider than the points \(A_k(x_k,f(x_k))\) and conclude that the polygonal passing through the \(A_k\)’s, i.e. \[g(x) = \begin{cases} 0 & (x=0)\\ 10^{-k}\left(x-\frac{10^{2k}}{11}\right) + 10^k & \frac{10^{2k}}{11}<x\leq \frac{10^{2k+2}}{11}, \ \forall k\in \Bbb Z\end{cases}\] is such that \(g(x)\geq f(x)\), with equality only for \(x= 0\) and for \(x=x_k\), \(k\in\Bbb Z\).
- Consider the concave function \[g(x) = \sqrt{11 x}.\] Observe that \(g\) passes through the points \(A_k\). Conclude that any function \[h(x) = K\sqrt x,\] with \(K>\sqrt{11}\), has no intersections with \(f\) other than \(x=0\), despite being continuous in \([0, +\infty)\) and differentiable in \((0, +\infty)\).
