The problem, presented in a previous post, of determining the point on a circumference that is closest to a given interior point \(P\), changes radically if we consider an ellipse, instead of a circle, even if we limit ourself to the case where the point \(P\) lies on the major axis.
Consider the ellipse with equation
\[ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\]
with \(a>b\), and a point \(P\) inside it with coordinates \(P(x_P,0)\), with \(x_P\leq a\). We wish to find the points on the ellipse that have minimum distance from \(P\), and the amount of such distance.
The locus of points having a given distance from \(P\) is a circumference centered in \(P\). So, we should look for the larger circle entirely contained inside the ellipse, i.e. tangent to the ellipse. The tangent points \(Q_1\) and \(Q_2\) are the points we are looking for, as depicted in the Figure below.
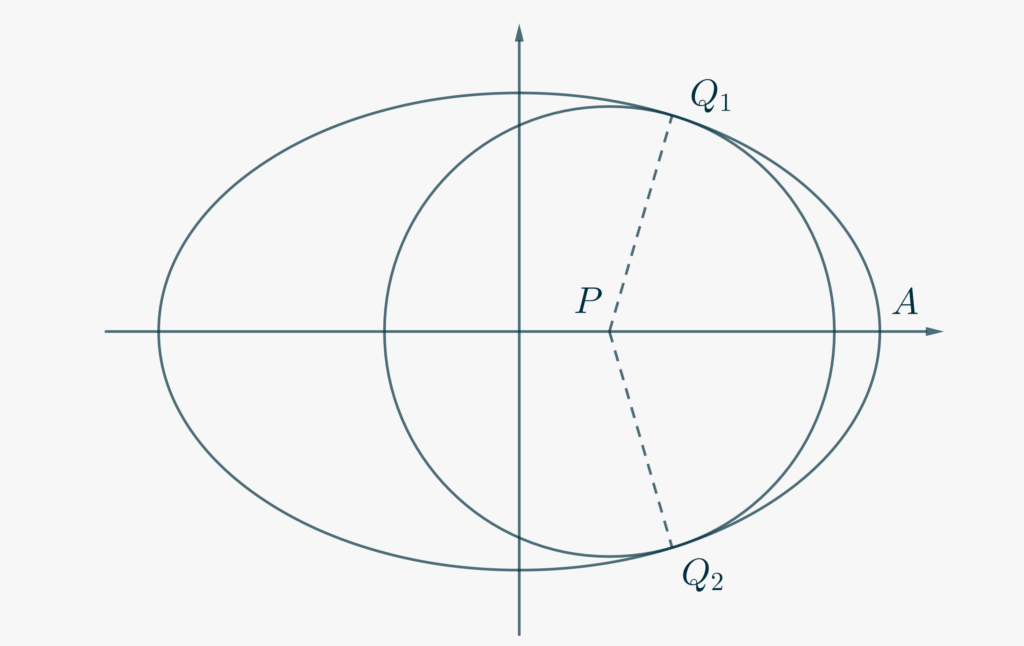
Let us consider the circumference with center in \(P\) and radius \(r\), whose equation is
\[(x-x_P)^2+y^2 = r^2.\]
The intersection points between circle and ellipse are found by solving the system of equations
\begin{equation}\begin{cases}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\
(x-x_P)^2+y^2 = r^2. \end{cases}\tag{1}\label{eq578:1}\end{equation}
Determining \(y^2\) from the second equation and plugging it into the first one leads to the second order equation
\begin{equation}x^2\left(\frac{1}{b^2}-\frac{1}{a^2}\right) -\frac{2x_P}{b^2}x-\frac{r^2-x_P^2-b^2}{b^2} = 0.\tag{2}\label{eq578:2}\end{equation}
For the desired radius, the circumference meets the ellipse at only two points having the same abscissa. Thus the above equation must have only one valid solution, which necessarily occurs if its discriminant is equal to zero, meaning
\[\frac{x_P^2}{b^4}+\left(\frac{1}{b^2}-\frac{1}{a^2}\right)\frac{r^2-x_P^2-b^2}{b^2} = 0\]
Solving with respect to \(r\) gives
\begin{equation}r^2 =b^2 -\frac{b^2}{a^2-b^2}x_P^2.\tag{3}\label{eq578:3}\end{equation}
For this value of \(r\), equation \eqref{eq578:2} becomes a perfect square, having the only solution
\[x = x_P \cdot \frac{a^2}{a^2-b^2}.\]
Replacing this value of \(x\) into the circle equation yields the coordinates of \(Q_1\) and \(Q_2\).
As an exercise, you can test the correctness of this procedure with the ellipse of major semi-axis \(a=4\) and minor semi-axis \(b=2\). If \(P\) has coordinates \((1,0)\) you should find \(r=\sqrt{\frac{11}{3}}\),
\[Q_1\left(\frac{4}{3},
\frac{4\sqrt{2}}{3} \right) \]
and
\[Q_2\left(\frac{4}{3},
-\frac{4\sqrt{2}}{3} \right).\]
However, discriminant of \eqref{eq578:2} being null is only a sufficient condition for the system \eqref{eq578:1} to have only one valid solution. Why? Try to see what happens with the same ellipse and point \(P(\frac{7}{2},0)\). Check that in this case the closest point to \(P\) on the ellipse is \(A(a,0)\), and thus
\begin{equation}r = a-x_P.\tag{4}\label{eq578:4}\end{equation}
What is the range of values of \(x_P\) allowing you to use \eqref{eq578:3}? And when do you need to use \eqref{eq578:4} instead?
