Il problema, presentato in un precedente articolo, della ricerca del punto sulla circonferenza a distanza minima da un punto interno a essa, cambia non poco se invece di una circonferenza prendiamo in considerazione un’ellisse, anche solo limitandosi al caso in cui il punto interno si trova sul suo semiasse maggiore.
Sia data un’ellisse di equazione
\[ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\]
con \(a>b\) e un punto interno a essa di coordinate \(P(x_P, 0)\), con \(0\leq x_P\leq a\). Determinare le coordinate dei punti sull’ellisse che hanno distanza minima da \(P\) e il valore di tale distanza.
Soluzione.
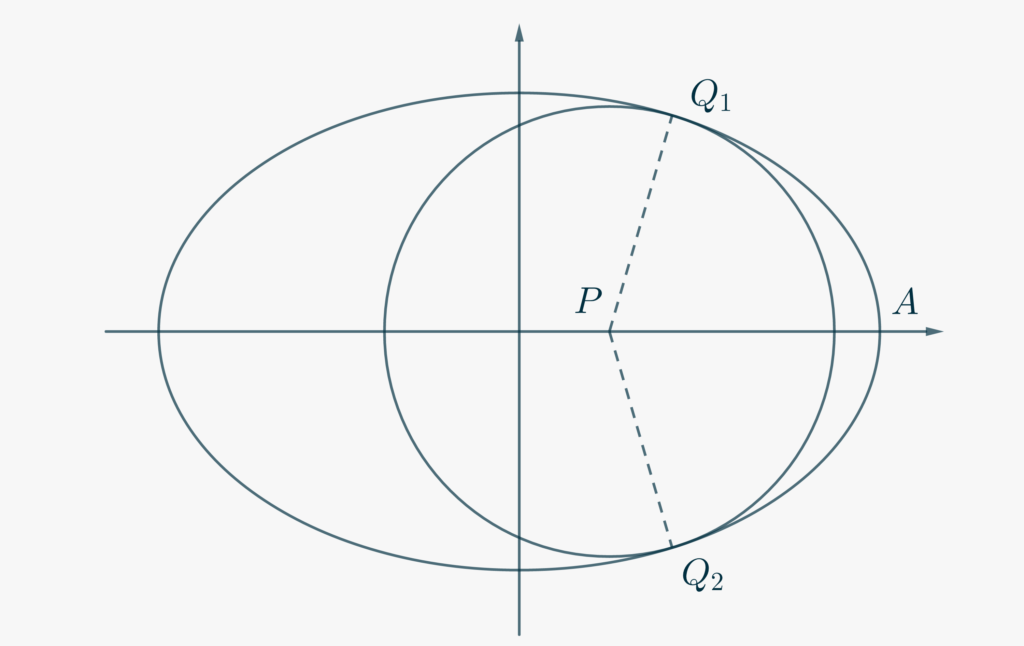
Considerando che il luogo dei punti a una data distanza da \(P\) è una circonferenza di centro \(P\), andremo alla ricerca della circonferenza di raggio massimo, interamente contenuta nell’ellisse, ovvero tangente all’ellisse. I punti di tangenza \(Q_1\) e \(Q_2\) saranno proprio i punti a distanza minima cercati, come mostrato in Figura.
L’equazione della circonferenza di centro \(P\) e raggio generico \(r\) è
\[(x-x_P)^2+y^2 = r^2.\]
La ricerca dei punti di intersezione tra circonferenza ed ellisse avviene come di consueto mettendone a sistema le equazioni, ovvero
\begin{equation}\begin{cases}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\\
(x-x_P)^2+y^2 = r^2. \end{cases}\tag{1}\label{eq117:1}\end{equation}
Ricavando \(y^2\) dalla seconda equazione e sostituendolo nella prima si ottiene una equazione di secondo grado in \(x\), che una volta ridotta in forma canonica risulta essere uguale a
\begin{equation}x^2\left(\frac{1}{b^2}-\frac{1}{a^2}\right) -\frac{2x_P}{b^2}x-\frac{r^2-x_P^2-b^2}{b^2} = 0.\tag{2}\label{eq117:2}\end{equation}
Dal momento che, per il valore del raggio desiderato, la circonferenza è tangente all’ellisse in punti con la medesima ascissa, questa equazione dovrà avere un’unica soluzione valida, il che è senz’altro vero nel caso in cui il suo discriminante sia uguale a \(0\):
\[\frac{x_P^2}{b^4}+\left(\frac{1}{b^2}-\frac{1}{a^2}\right)\frac{r^2-x_P^2-b^2}{b^2} = 0\]
Risolvendo rispetto a \(r\) ricaviamo
\begin{equation}r^2 =b^2 -\frac{b^2}{a^2-b^2}x_P^2.\tag{3}\label{eq117:3}\end{equation}
Per questo valore di \(r^2\), la \eqref{eq117:2} è un quadrato perfetto, che dà come unica soluzione per la \(x\)
\[x = x_P \cdot \frac{a^2}{a^2-b^2}.\]
Sostituendo infine questo valore nell’equazione dell’ellisse o della circonferenza, si ottengono le ordinate di \(Q_1\) e \(Q_2\).
Per esercizio, verifica la correttezza del procedimento, con l’ellisse avente semiasse maggiore \(a=4\) e semiasse minore \(b=2\). Se il punto \(P\) ha coordinate \((0,1)\), dovresti ottenere \(r=\sqrt{\frac{11}{3}}\), e, per i punti a distanza minima,
\[Q_1\left(\frac{4}{3},
\frac{4\sqrt{2}}{3} \right) \]
e
\[Q_2\left(\frac{4}{3},
-\frac{4\sqrt{2}}{3} \right).\]
Tuttavia l’annullamento del discriminante della \eqref{eq117:2}, è soltanto una condizione sufficiente, e non necessaria, all’esistenza di una sola soluzione per la \(x\) del sistema \eqref{eq117:1}. Perché? Prova a verificare cosa succede ponendo il punto \(P\) in \((\frac{7}{2},0)\). Verifica che in questo caso il punto più vicino a \(P\) sull’ellisse è \(A(a,0)\) e quindi
\begin{equation}r = a-x_P.\tag{4}\label{eq117:4}\end{equation}
Per quali valori di \(x_P\) devi usare la \eqref{eq117:3} per trovare la distanza minima? E per quali devi usare la \eqref{eq117:4}?