We are given a function \(f(x)\), for which the right derivative
\[f’_+(x) = \lim_{h\rightarrow 0^+}\frac{f(x+h)-f(x)}{h}\]
is defined in \(\Bbb R\). We also know that \(f’_+(x) \geq 0\) for all \(x\). Is this condition sufficient to conclude that the function is increasing “at the right of each point”, i.e. that \( \forall x \in \Bbb R\) there exists \(\delta >0\) such that
\[y\in (x,x+\delta) \Rightarrow f(y) \geq f(x)?\]
Surprisingly enough, the answer is no. Without continuity, the non-negativity of the right derivative is not sufficient to conclude that the function is increasing at the right of each point.
An interesting counterexample is depicted in the Figure below. Red lines have equations \(y=-x|x|\) and \(y=-\frac{1}{2}x|x|\).
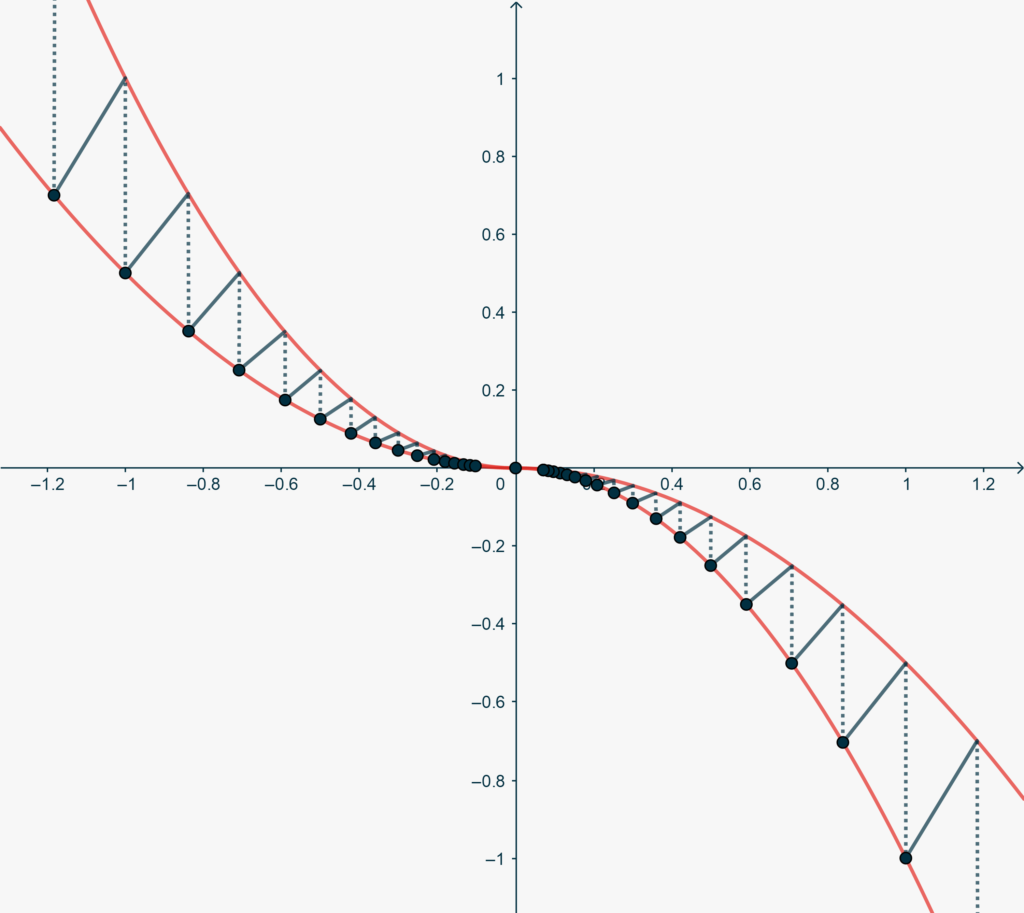
The function is then defined by means of portions of stright lines as folllows.
\[ f(x) = \begin{cases}\frac{\sqrt{2^{-k}}-\sqrt{2^{-k+1}}}{\sqrt[4]{2^{-k+1}}-\sqrt[4]{2^{-k}}}(x+\sqrt[4]{2^{-k+1}})- \sqrt{2^{-k+1}} & \left(-\sqrt[4]{2^{-k+1}}\leq x<-\sqrt[4]{2^{-k}}; \ k\in \Bbb Z\right)\\ 0 & (x=0)\\ \frac{\sqrt{2^{-k}}-\sqrt{2^{-k+1}}}{\sqrt[4]{2^{-k+1}}-\sqrt[4]{2^{-k}}}(x-\sqrt[4]{2^{-k+1}})+ \sqrt{2^{-k+1}}& \left(\sqrt[4]{2^{-k}}\leq x<\sqrt[4]{2^{-k+1}}; \ k\in \Bbb Z\right) .\end{cases}\]
It is easy to verify that the right derivative is defined and striclty positive at the right of each point for \(x\neq 0\).
As for the behavior of \(f(x)\) in \(0\), observe that
\begin{equation}\left|f(x)\right| \leq x^2\tag{1}\label{eq597:1}\end{equation}
and thus
\begin{equation}\left|\frac{f(x)}{x}\right| \leq |x|.\tag{2}\label{eq597:2}\end{equation}
From \eqref{eq597:1} and the squeezing rule we have
\[\lim_{x\rightarrow 0} f(x) = 0 = f(0).\]
Therefore the function is continuous in \(0\). Furthermore, by \eqref{eq597:2} and again the squeezing rule,
\[f'(0) = \lim_{x\rightarrow 0}\frac{f(x)}{x} = 0,\]
so that \(f(x)\) is also differentiable in \(0\), with \(f'(0)=0\). However in every right neighborhood of \(0\) the function is negative, i.e. \(f(x)<0\) for all \(x>0\).
In a next post we will show that adding continuity to the hypotheses, will allow us to answer affirmatively to the original question.
