In this post we will investigate the connection between slant asymptotes and the behavior of the derivative at \(\infty\) for differentiable real functions.
We say that a function \(f(x)\) has a slant asymptote \(y=mx +q\) for \(x\to+\infty\) whenever
\begin{equation}\lim_{x\to+\infty} \underbrace{\left[f(x)-mx-q\right]}_{D(x)} = 0,\tag{1}\label{eq2624:1}\end{equation}
i.e. the distance \(D(x)\) between the function and the straight line of equation \(y=mx+q\) tends to \(0\) as \(x \to +\infty\).
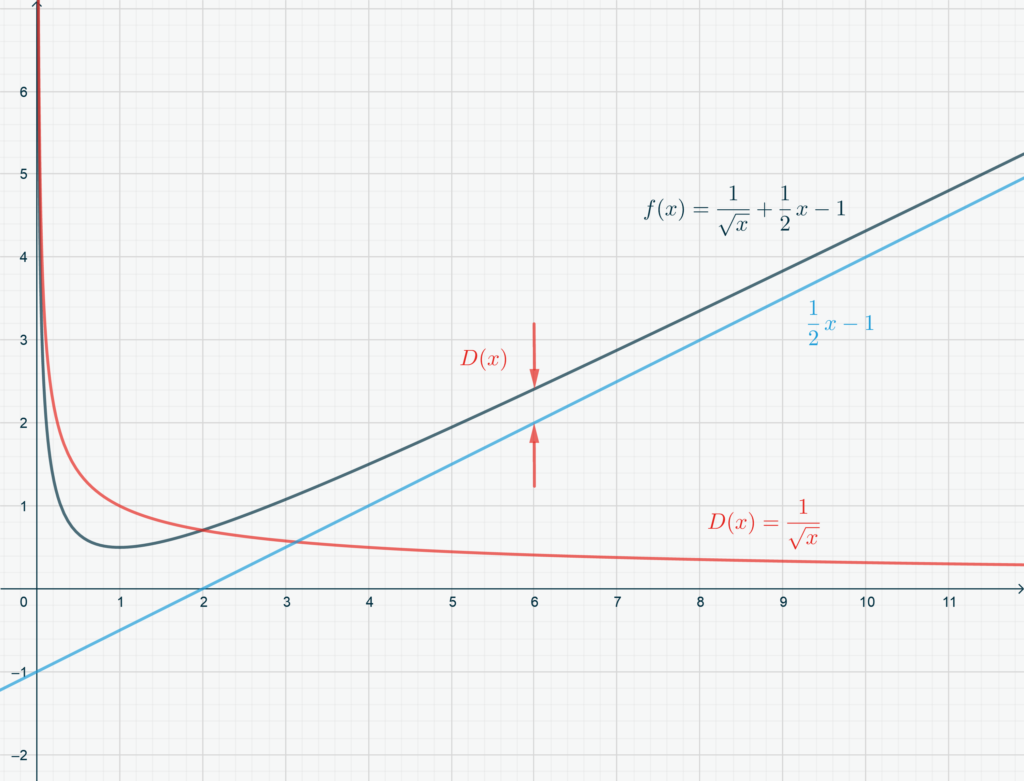
In the Figure below a very simple example is depicted, where \(f(x) = \frac1{\sqrt x} + \frac12 x -1\) is the dark blue line and the asymptote \(y = \frac12 x -1\) is the light blue line. Marked in red, you can see the distance between \(f(x)\) and the straight line, that is
\[D(x) = f(x)-mx-q = \frac1{\sqrt x}.\]
Suppose that equation \eqref{eq2624:1} is satisfied. Then we have
\begin{eqnarray}\lim_{x\to+\infty} \frac{f(x)}{x}&=&\lim_{x\to+\infty} \frac{D(x)+mx+q}{x}=\\&=&\lim_{x\to+\infty} \frac{D(x)}{x} +m = m \tag{2}\label{eq2624:2}\end{eqnarray}
Thus, \eqref{eq2624:2} is a necessary condition for the existence of an asymptote. This leads to a straightforward procedure:
- Calculate the limit \eqref{eq2624:2}. If this limit does not exist or it is infinite, then the function does not have an asympote. If the limit exists and is finite, then there might be an asymptote with slope \(m\).
- If you found a finite \(m\), then you also need to compute the limit \begin{equation}\lim_{x\to+\infty} \left[f(x)-mx\right].\tag{3}\label{eq2624:3}\end{equation}If this limit, too, exists and is finite (call it \(q\)) you can conclude that the function does have an asympote with equation \(y = mx + q\).
As an exercise, test this method with the function
\[f(x) = (x-2) e^{-\frac1x}.\]
You should find the asymptote \(y=x-3\).
Suppose now the function \(f(x)\) is differentiable, at least in a neighborhood of \(+\infty\). We ask ourselves if there is any connection between the potential slant asyptote and the behavior of the derivative at infinity. By De l’Hôpital’s rule, we know that, if
\begin{equation}\lim_{x\to+\infty} f'(x)\tag{4}\label{eq2624:4}\end{equation}
exists (whether finite or infinite), then it is equal to
\[\lim_{x\to+\infty} = \frac{f(x)}{x}.\]
Therefore,
- If limit \eqref{eq2624:4} exists and is infinite, then, by necessity of condition \eqref{eq2624:2} we conclude that the function does not have an asyptote.
- If limit \eqref{eq2624:4} exists and is finite, then the function may or may not have an asymptote, depending on the limit \eqref{eq2624:3}.
- If limit \eqref{eq2624:4} does not exist, again no conclusion can be drawn, and we need to test both limits \eqref{eq2624:2} and \eqref{eq2624:3}.
Here are some exercises to conclude our discussion.
- Consider \[f(x) = \log x + x.\]Show that the limit \eqref{eq2624:4} (and thus \eqref{eq2624:2}) exists and is finite, and that, however, \(f(x)\) does not have a slant asympote.
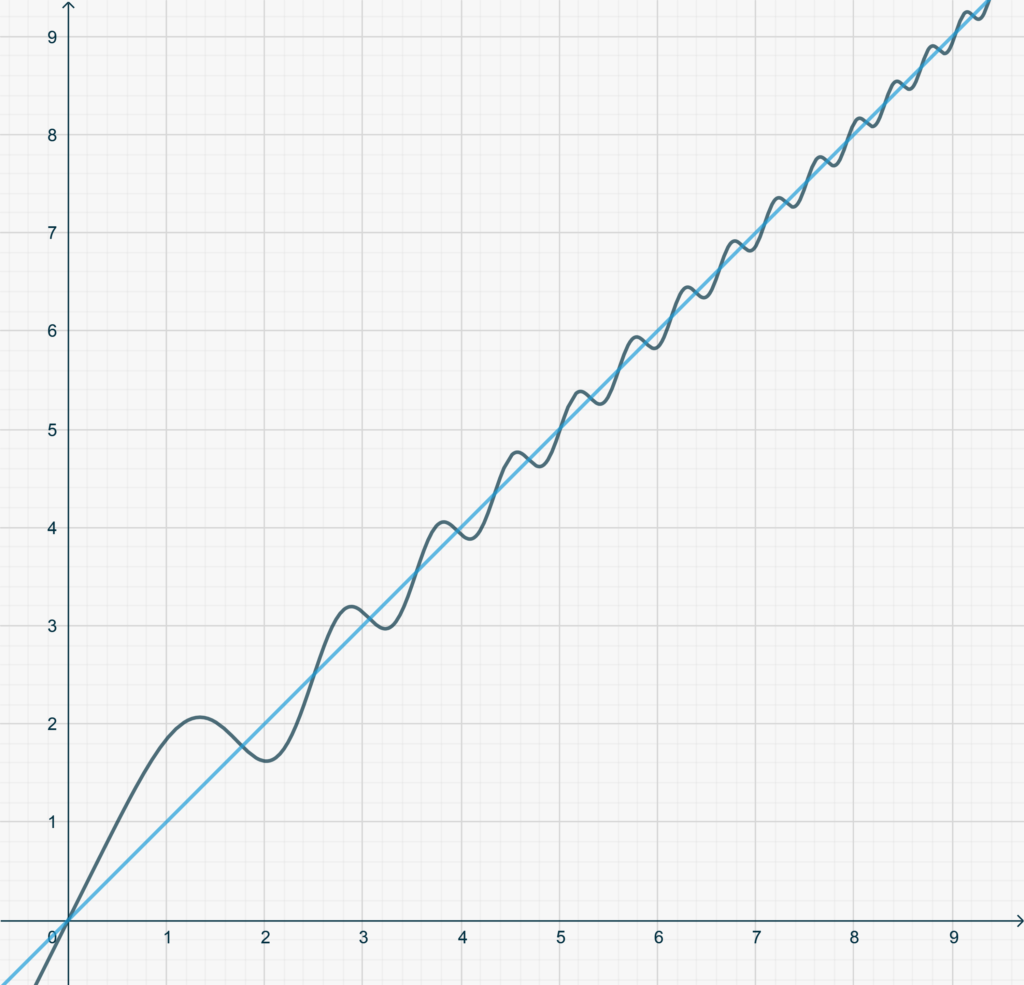
- Let \[f(x) = \frac{\sin x^2}{x}+x.\] Show that this function has a slant asymptote even though the limit \eqref{eq2624:4} does not exist. The function is represeted in the Figure below, together with its asymptote.
- Modify the function of the previous exercise, so that it has a slant asymptote, but unbounded derivative in every neighboorhood of \(+\infty\).
- In the two previous examples the distance \(D(x)\) between the function and the asymptote is not monotonic. Construct then an example of a function that monotonically tends to its asymptote (that is: \(D(x)\) is monotonic) and yet has unbounded derivative in every neighborhood of \(+\infty\).
