This post is devoted to Menelaus’s Theorem, named for the astronomer Menelaus of Alexandria. It is a very imporant theorem in geometry, relating the ratios of the segments obtained by “cutting” the sides of a triangle (or their extensions) with a straight line. Once you become familiar with it, you’ll find that it is very useful in solving efficienlty a wide range of problems that otherwise would require coordinate geometry and trigonometry.
Theorem. Consider a triangle \(\triangle ABC\) and a line not passing through the triangle vertices. Let \(D\), \(E\) and \(F\) its intersections with (the extension) of \(BC\), \(AC\), and \(AB\) respectively, then
\begin{equation}\frac{\overline{AF}}{\overline{FB}}\cdot \frac{\overline{BD}}{\overline{DC}}\cdot \frac{\overline{CE}}{\overline{EA}} = 1.\tag{1}\label{eq803:1}\end{equation}
The complete version of the Theorem, actually, states that the given ratio is a necessary and sufficient condition for the collinearity of points \(D\), \(E\), and \(F\). Its demonstration is straightforward, and it is based on similarities among auxiliary triangles.
Let us practice the use of this Theorem with a first, simple, exercise.
From vertex \(A\) of triangle \(\triangle ABC\) consider a line that intersects the opposite side \(BC\) in \(D\), and from vertex \(B\) a line that intersects \(AC\) in \(E\). Let \(P\) the interesections between these lines. Suppose the area of \(\triangle ABP\) is equal to \(6\), the area of \(\triangle AEP\) is equal to \(3\), and the area of \(\triangle BDP\) is \(4\). Determine the area of the quadrilateral \(CDPE\).
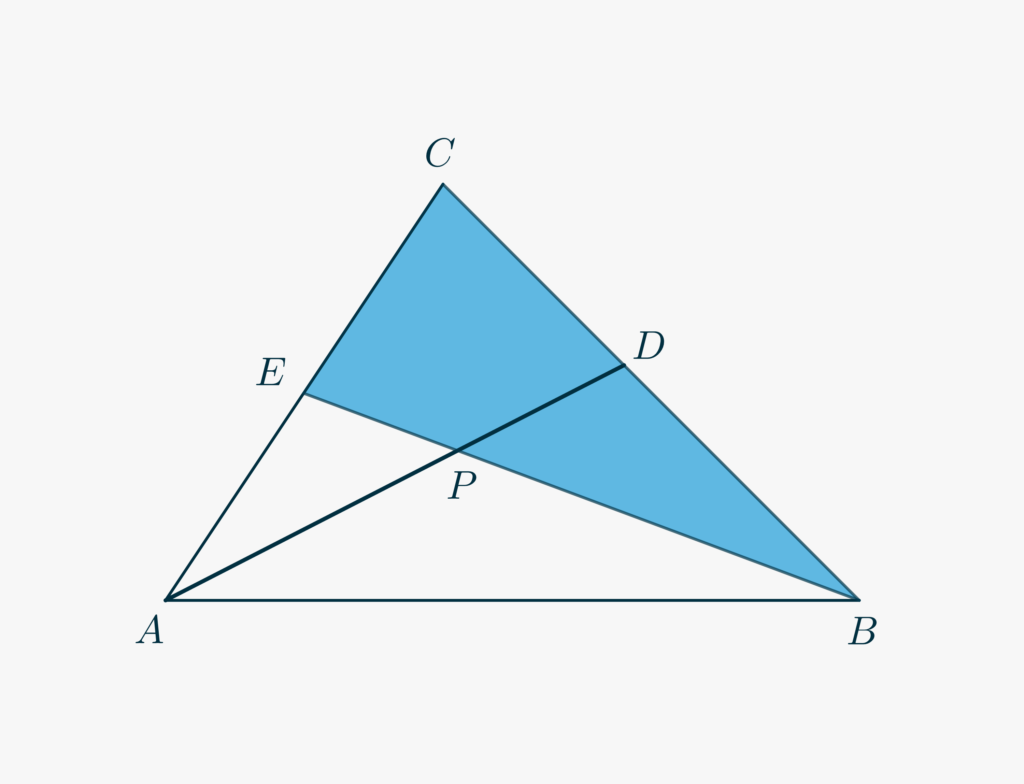
- Let \(x\) be the unknown area of \(CDEP\).
- In order to determine it, we will apply Menelaus’s Theorem to triangle \(\triangle BEC\) cut by \(AD\). So we have
\begin{equation}\frac{\overline{EP}}{\overline{PB}}\cdot\frac{\overline{BD}}{\overline{DC}}\cdot\frac{\overline{AC}}{\overline{AE}}=1.\tag{2}\label{eq803:2}\end{equation} - Our first aim is therefore writing LHS of \eqref{eq803:2} as a function of \(x\).
- Observe that the ratios of the areas of \(\triangle AEP\) and \(\triangle ABP\) is equal to \(\frac{\overline{PE}}{\overline{PB}}\). Why?
- Apply the same idea to the ratio between the areas of \(\triangle ABD\) and \(\triangle ADC\), which are respetively equal to \(10\) and \(3+x\), and thus obtain \(\frac{\overline{BD}}{\overline{DC}} = \frac{10}{3+x}\).
- Again use the same approach on triangles \(\triangle ABC\) and \(\triangle ABE\) to express the ratio \(\frac{\overline{AC}}{\overline{AE}}\) as a function of \(x\).
- Use the previous results in \eqref{eq803:2} and solve the equation. You will find \(x = \frac{19}{2}\).
We are ready now to approach a more structured exercise, that will better emphasize the efficiency of the method.
Let \(\triangle ABC\) be an equilater triangle, and \(P\) a point on the circumscribed circle. Let also \(D\), \(E\), and \(F\) be the intersections of \(PA\) with line \(BC\), \(BP\) with line \(AC\) and \(PC\) with line \(AB\), respectively. Prove that the area of \(\triangle DEF\) is twice the area of \(\triangle ABC\).
Without loss of generality suppose \(P\) lies in the half-plane determined by \(BC\) and not containing \(A\). We can also assume \(\overline{AB} = 1\). In following the notation \([\cdots]\) will be used to indentify the area of the polygon whose vertices are listed in brackets.
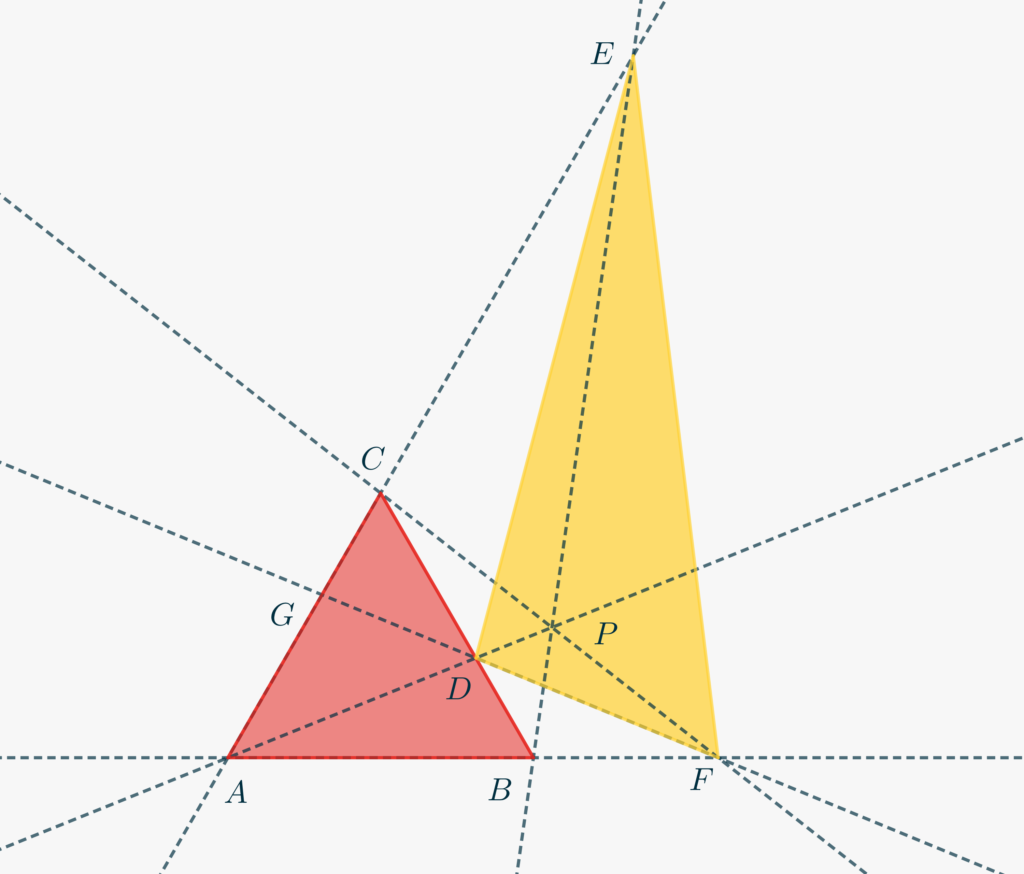
- Observe that we can completely forget about the circle, since \(P\) belonging to it is just equivalent to stating that \(\angle CPB = 120°\). Why?
- Let us call \(\overline{BF} = x\). Note that, once \(x\) is fixed, the entire Figure is defined, so that our aim can be restated as computing \([DEF]\) as a function of \(x\), and thus show that the result is eventually independent of \(x\).
- We will first need some segment measures in \(\triangle BCF\). The picture below, where \(CK\), perpendicular to \(AB\) has been drawn, shows all the details required.
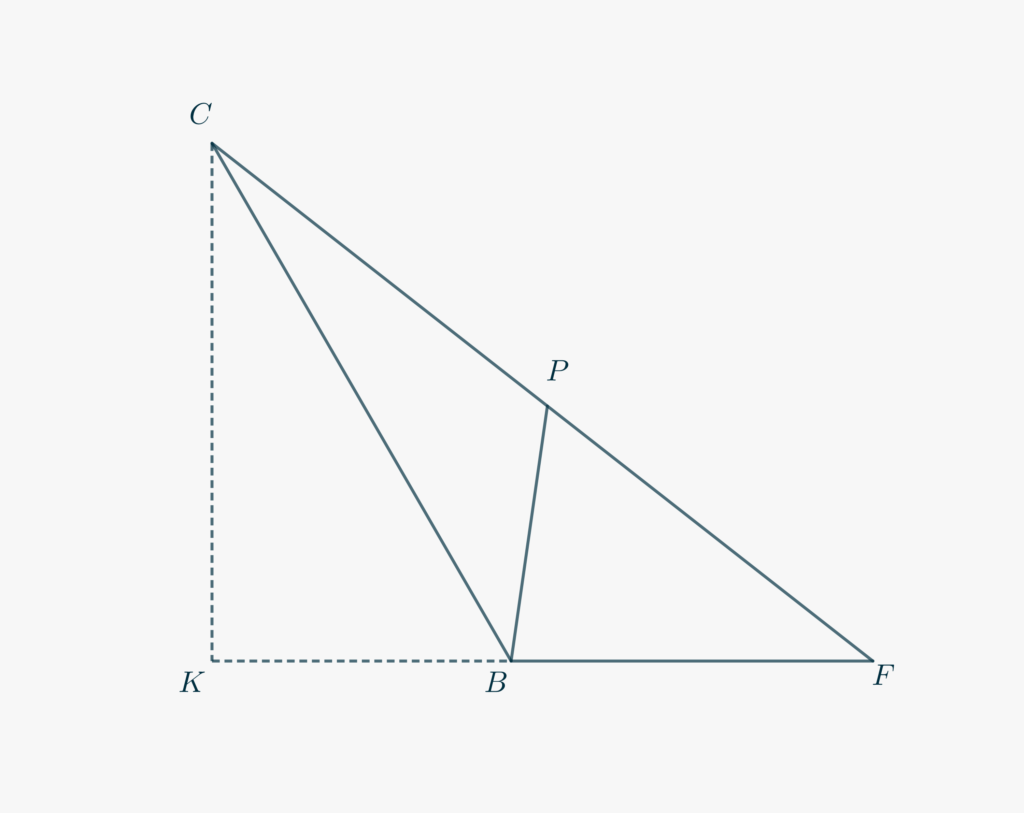
- Prove that \(\triangle BCF\) and \(\triangle BCP\) are similar.
- Use this fact to show that \begin{equation}\overline{CP}\cdot\overline{FC}= 1.\tag{3}\label{eq803:3}\end{equation}
- Observe that \(\triangle CKB\) is half of an equilateral triangle. Compute then \(\overline{BK}\) and \(\overline{KF}\).
- Determine \(\overline{FC}\) via Pythagorean Theorem. You should obtain \[\overline{FC} = \sqrt{x^2+x+1}.\]
- Use \eqref{eq803:3} to compute \[\overline{CP}= \frac{1}{\sqrt{x^2+x+1}}\] and \[\overline{FP} = \frac{x(x+1)}{\sqrt{x^2+x+1}}.\]
- Getting back to the initial Figure, we can now repeatedly apply Menelaus’s Theorem to calculate all other segment lenghts we need. Start with \(\triangle ACF\), cut by line \(BE\). This will lead to \[\frac{\overline{CE}}{\overline{AE}} = \frac{1}{x+1}.\] Since we have \(\overline{AE} – \overline{CE} = 1\), we can get \(\overline{AE} = \frac{1}{x}\) and \(\overline{CE} = \frac{x+1}{x}\).
- Again our Theorem on \(\triangle BFC\) and line \(AP\), together with the information \(\overline{BD}+\overline{CD}=1\), allows you to compute \(\overline{CD}\) e \(\overline{BD}\). Check your result with the following: \(\overline{CD} = \frac{1}{x+1}\) and \(\overline{BD} = \frac{x}{x+1}\).
- Switch now to \(\triangle ABC\), intercepted by \(FG\), and, using the Theorem and the relationship \(\overline{AG} + \overline{CG} = 1\), determine \(\overline{AG} = \frac{x+1}{x+2}\) and \(\overline{CG} = \frac{1}{x+2}\).
- One last application of Menelaus’s Theorem to \(\triangle CGF\) and line \(AP\), will lead you to the ratio \[\frac{\overline{GD}}{\overline{DF}} = \frac{1}{x(x+2)}.\]
- Recalling the first exercise, we can go backward and use segment lengths to determine areas of triangles of fixed altitude and a known ratio between bases. Start with \(\triangle ACF\) that shares with \(ABC\) the altitude relative to \(AF\). This implies \[[ACF] = [ABC](1+x).\]
- \(\triangle AFE\) and \(\triangle ACF\) have the altitude relative to \(AE\) in common. Thus \[[AFE] = [ACF] \cdot \frac{\overline{AE}}{\overline{AC}}.\] Check that this leads to \[[AFE] = [ABC]\cdot \frac{(x+1)^2}{x}.\]
- Do the same with \(\triangle GFE\) and \(\triangle AFE\) to obtain \begin{equation}[GFE] = [ABC]\cdot\frac{2(x+1)^2}{x(x+2)}.\tag{4}\label{eq803:4}\end{equation}
- At last, observe that \begin{equation}\frac{[DFE]}{[GDE]} = \frac{\overline{GD}}{\overline{DF}} = \frac{1}{x(x+2)}\tag{5}\label{eq803:5}\end{equation} and that \begin{equation}[DFE] + [GDE] = [GFE]\tag{6}\label{eq803:6}.\end{equation} Replace \eqref{eq803:4} in \eqref{eq803:6}. Determine from the latter equation \([GDE]\) and replace it in \eqref{eq803:5}. You will get an equation with \([DEF]\) as unknown, which, once solved, will give you \[[DEF] = 2[ABC],\] as expected.
