In questo post, nel contesto di funzioni reali di variabile reale, investighiamo il collegamento esistente tra la presenza di un asintoto obliquo e il comportamento della derivata all’infinito
Diciamo che una funzione \(f(x)\) ha un asintoto obliquo \(y=mx+q\) quando
\begin{equation}\lim_{x\to+\infty} \underbrace{\left[f(x)-mx-q\right]}_{D(x)} = 0,\tag{1}\label{eq2622:1}\end{equation}
ovvero quando la distanza \(D(x)\) tra la funzione e la retta di equazione \(y=mx + q\) tende a \(0\) quando \(x\) tende a infinito.
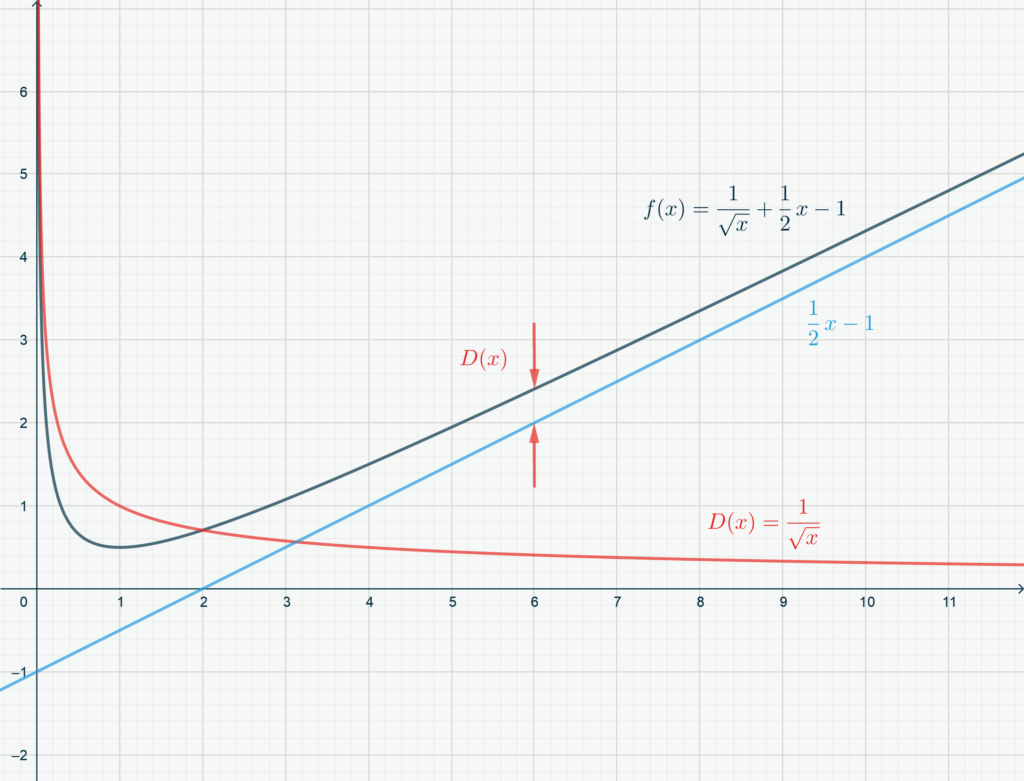
La Figura qui sotto mostra un semplice esempio, dove \(f(x) =\frac1{\sqrt x} + \frac12 x -1\) è la linea blu scuro e l’asintoto \(y = \frac12 x -1\) è la linea azzurra. In rosso è evidenziata la distanza tra i due grafici, cioè
\[D(x) = f(x)-mx-q = \frac1{\sqrt x}.\]
Supponiamo che l’equazione \eqref{eq2622:1} sia soddifatta. Allora
\begin{eqnarray}\lim_{x\to+\infty} \frac{f(x)}{x}&=&\lim_{x\to+\infty} \frac{D(x)+mx+q}{x}=\\&=&\lim_{x\to+\infty} \frac{D(x)}{x} +m = m \tag{2}\label{eq2622:2}\end{eqnarray}
Concludiamo che \eqref{eq2622:2} è una condizione necessaria all’esistenza di un asintoto obliquo. Questo ci fornisce una semplice strategia per verificare se una data funzione \(f(x)\) possiende un asintoto obliquo e, in caso affermativo, per trovarne l’equazione.
- Calcoliamo il limite \eqref{eq2622:2}. Se esso non esiste o è infinito, allora la funzione non ammette asintoto. Se invece il limite esiste finito, allora la funzione potrebbe avere un asintoto di coefficiente angolare \(m\).
- Una volta trovato \(m\), occorre infatti calcolare anche il limite \begin{equation}\lim_{x\to+\infty} \left[f(x)-mx\right].\tag{3}\label{eq2622:3}\end{equation}Se anche questo limite esiste finito, ed è pari a \(q\), allora concludiamo che la funzione ha asintoto di equazione \(y = mx + q\).
Come esercizio, puoi utilizzare la procedura appena descritta sulla funzione
\[f(x) = (x-2) e^{-\frac1x}.\]
Dovresti trovare un asintoto di equazione \(y=x-3\).
Supponiamo ora che \(f(x)\) sia derivabile, per lo meno in un intorno di \(+\infty\). Ci chiediamo allora se esista qualche collegamento tra il comportamento della derivata all’infinito e l’eventuale presenza di asintoti. Dalla regola di De l’Hôpital sappiamo che, se
\begin{equation}\lim_{x\to+\infty} f'(x)\tag{4}\label{eq2622:4}\end{equation}
esiste (finito o infinito), allora è uguale a
\[\lim_{x\to+\infty} = \frac{f(x)}{x}.\]
Quindi
- Se il limite \eqref{eq2622:4} esiste ed è infinito, allora, essendo la condizione \eqref{eq2622:2} necessaria, deduciamo che la funzione non ha asintoto.
- Se il limite \eqref{eq2622:4} esiste finito, allora la funzione potrebbe o meno avere un asintoto, a seconda del risultato del limite \eqref{eq2622:3}.
- Anche se il limite \eqref{eq2622:4} non esiste non possiamo trarre alcuna conclusione; occorrerà calcolare entrambi i limiti \eqref{eq2622:2} and \eqref{eq2622:3}.
Concludiamo con qualche esercizio di approfondimento.
- Considera la funzione \[f(x) = \log x +x.\]Mostra che il limite \eqref{eq2622:4} (e quindi anche \eqref{eq2622:2}) esiste finito e che ciononostante \(f(x)\) non ammette asintoto.
- Dimostra che \[f(x) = \frac{\sin x^2}{x}+x,\] ammette asintoto obliquo malgrado il limite \eqref{eq2622:4} non esista. La funzione è rappresentata qui sotto, insieme al suo asintoto.
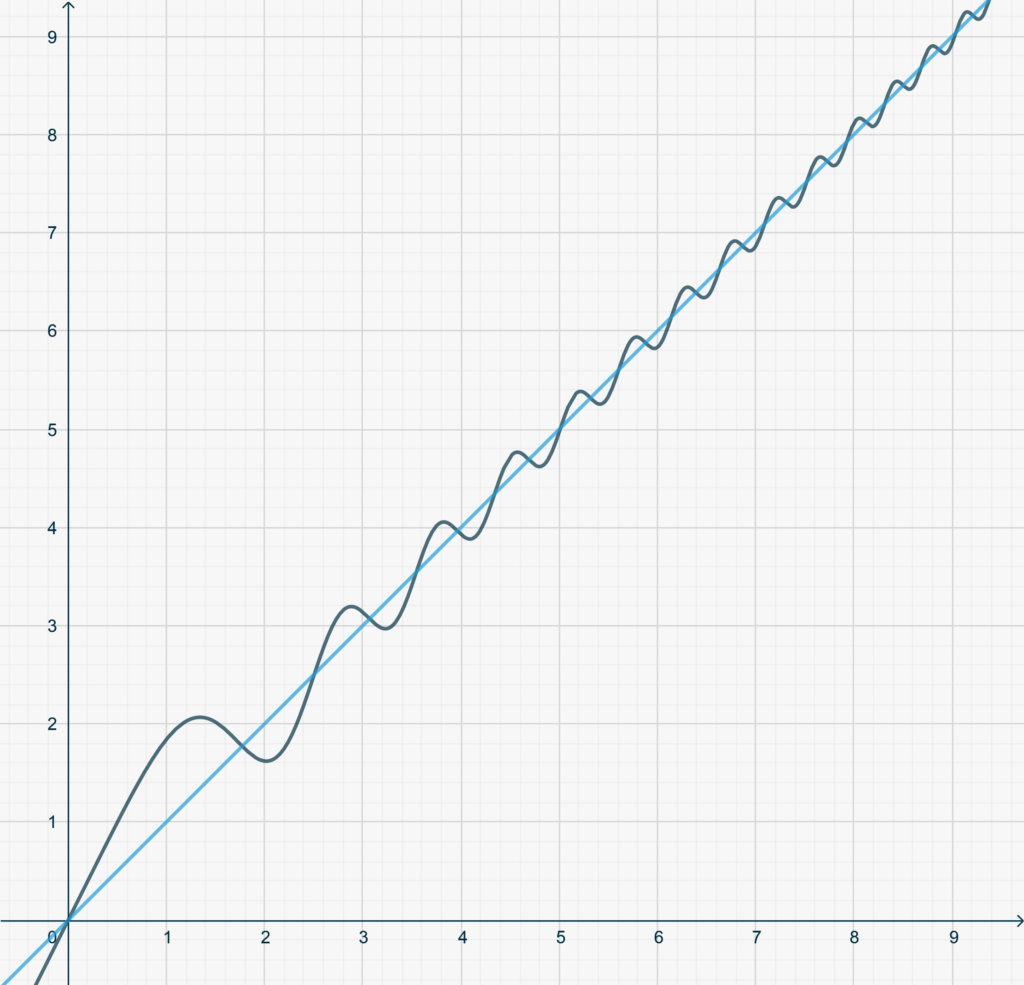
- Modifica la funzione dell’esercizio precedente affinché la funzione abbia asintoto obliquo ma derivata illimitata in ogni intorno di \(+\infty\).
- Nei due esempi precedenti, la distanza \(D(x)\) tra la funzione e l’asintoto non è monotona. Costruisci un esempio di funzione che tende monotonicamente al proprio asintoto obliquo (ovvero \(D(x)\) è monotona), ma la cui derivata è illimitata in ogni intorno di \(+\infty\).