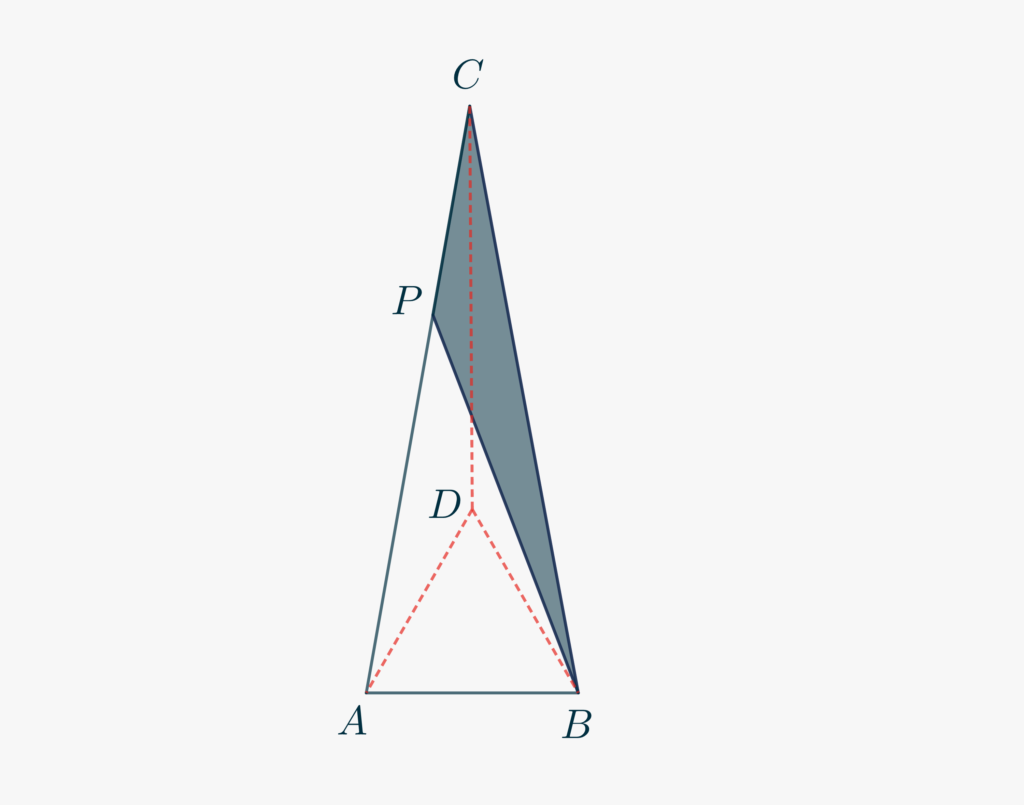
Presentiamo ancora un problema di geometria euclidea, con soluzione guidata. Un “classico”, relativo al triangolo isoscele “\(80-80-20\)”.
Dato un triangolo isoscele \(\triangle ABC\) con angoli alla base \(\angle ABC = \angle BAC = 80°\), si prenda sul segmento \(AC\) un punto \(P\) in modo che sia \(CP\cong AB\). Quanto misura l’angolo \(\angle CPB\)?
Per poter sfruttare la congruenza tra i segmenti \(AB\) e \(CP\), è necessario costruire altri triangoli. Una possibile soluzione è quella di disegnare due repliche di \(\triangle ABC\), adiacenti una all’altra, come nella Figura sottostante, dove \(\triangle ABC\cong \triangle BCD \cong \triangle CDE\).
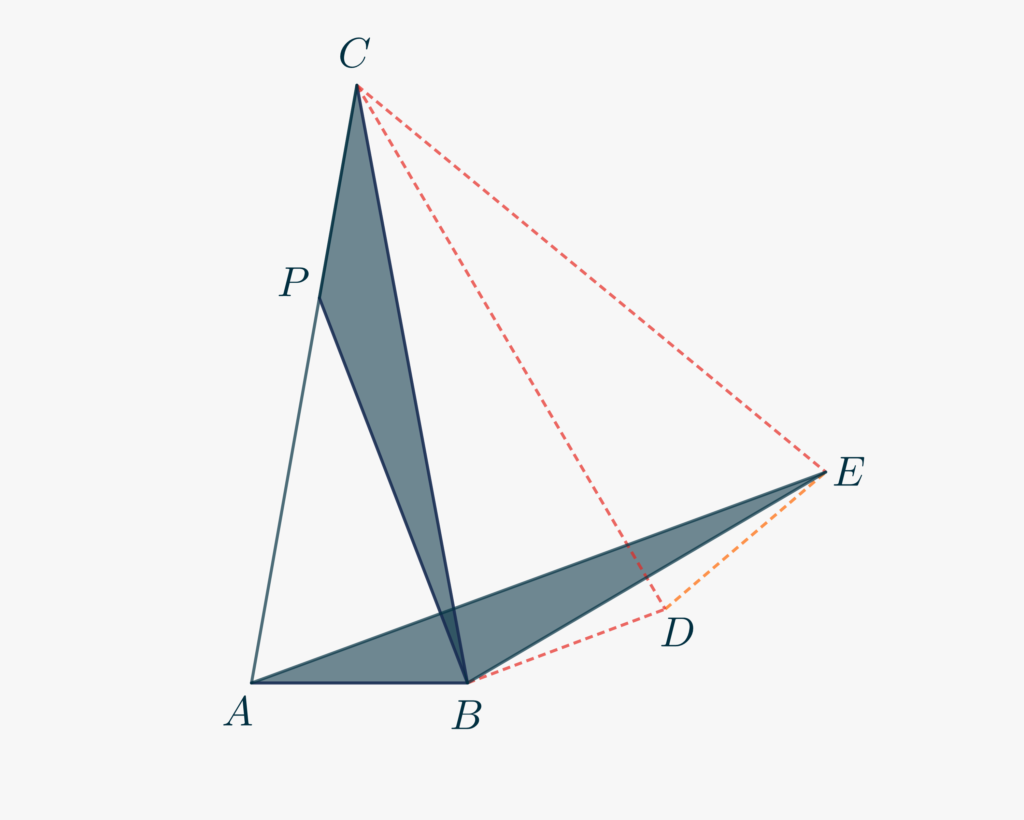
- Il triangolo \(\triangle ACE\), per costruzione, è isoscele. Quanto misura l’angolo al vertice \(\angle ACE\)?
- Cosa puoi concludere, quindi, relativamente al triangolo \(\triangle ACE\)?
- Determina, per sottrazione, la misura dell’angolo \(\angle EAB\).
- Osserva che i dati che hai a disposizione sono sufficienti per concludere che \(\triangle CPB\) e \(\triangle AEB\) sono congruenti. Mediante quale criterio?
- Dobbiamo ora determinare la misura di \(\angle CPB\cong\angle ABE\).
- Concentrati sul triangolo \(\triangle BDE\). Di che triangolo si tratta? Perché? Usa questa informazione per determinare la misura di \(\angle DBE\).
- Componendo opportunamente la misura di angoli noti, determina quella di \(\angle ABE\) e quindi la risposta alla domanda. Otterrai \(\angle CPB = 150°\).
Come ulteriore esercizio, prova dimostrare di nuovo l’asserto, questa volta utilizzando la costruzione riportata qui sotto, in cui \(\triangle ADB\) è equilatero