Come abbiamo visto in un post precedente, le identità che coinvolgono l’arcotangente risultano assai meno misteriose se osservate da un punto di vista strettamente geometrico. In questo articolo avrai l’occasione di fare ulteriore pratica e di ottenere un’interessante generalizzazione. Cominciamo con la relazione
\begin{equation}\arctan x + \arctan\left(\frac{x+1}{x-1}\right) =\frac{3\pi}{4}, \ \ \mbox{per}\ \ x>1.\tag{1}\label{eq280:1}\end{equation}
Partiremo dall’ormai consueto triangolo rettangolo \(\triangle ABC\) con cateti di lunghezza pari a \(\overline{AB}=1\) e \(\overline{BC} = x\), e con ipotenusa \(\overline{AC} = \sqrt{1+x^2}\).
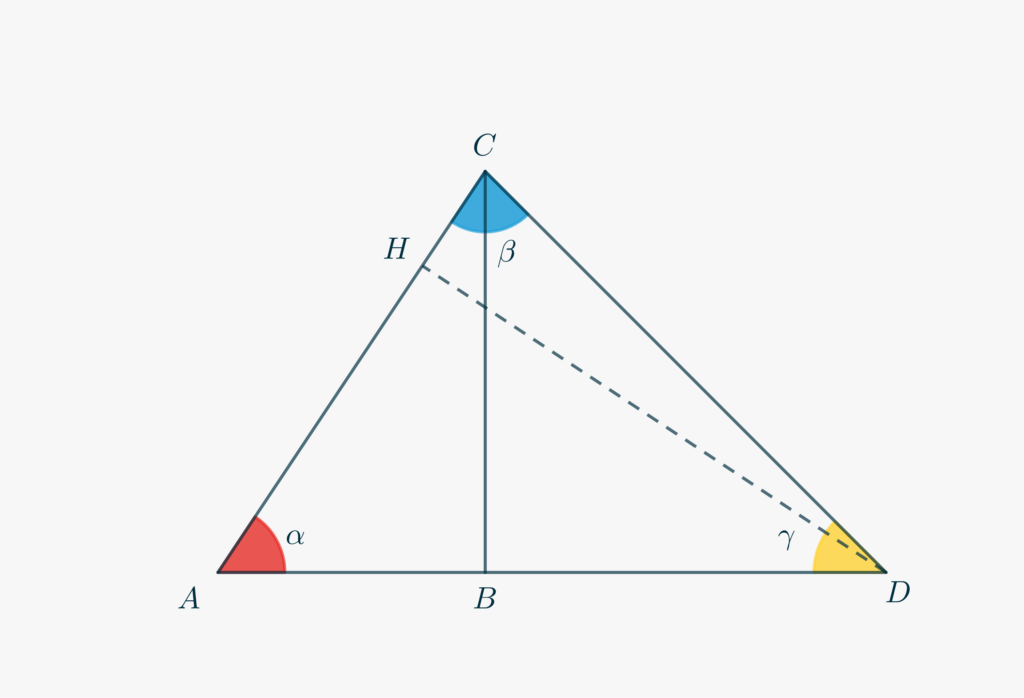
- Prolunga \(AB\) dalla parte di \(B\) con un segmento \(\overline{BD} = x\).
- Il triangolo \(\triangle BCD\) è isoscele. Cosa puoi dedurre relativamente all’angolo \(\gamma = \angle ADC\)?
- Usando quanto hai osservato, e il fatto che la somma degli angoli interni di \(\triangle ABC\) è \(\pi\), scrivi \(\beta = \angle ACD\) in funzione di \(\alpha\). Dovresti ricavare \[\beta = \frac{3\pi}{4}-\alpha.\]
- Traccia da \(D\) la perpendicolare ad \(AC\), che interseca \(AC\) in \(H\).
- Il triangolo \(\triangle ADH\) è simile a \(\triangle ABC\). Perché?
- Dal rapporto di similitudine tra questi due triangoli e dal fatto che \(\overline{AD} = 1+x\), determina \(\overline{DH}\), \(\overline{AH}\) e infine \(\overline{CH} = \overline{AC}-\overline{DH}\).
- Scrivi \(\beta\) come \(\arctan\left(\frac{\overline{DH}}{\overline{CH}}\right)\).
- Utilizzando la relazione tra \(\alpha\) e \(\beta\) trovata nel punto 3., ricava l’identità \eqref{eq280:1}.
Se hai seguito la dimostrazione precedente non dovresti avere difficoltà a dimostrare anche l’identità
\begin{equation}\arctan x + \arctan\left(\frac{\sqrt 3 x+1}{x-\sqrt 3}\right)=\frac{5\pi}{6}, \ \ \mbox{per} \ \ x >\sqrt 3.\tag{2}\label{eq280:2}\end{equation}
Si tratterà di modificare la misura dell’angolo \(\gamma\), in modo che sia uguale a \(\frac{\pi}{6}\). Quanto è lungo, allora, il segmento \(BD\) (ricorda che \(\frac{\pi}{3}\) è la misura degli angoli interni di un triangolo equilatero)? Procedi poi, da qui, seguendo i passi della dimostrazione precedente.
A questo punto potresti domandarti se la procedura sia ulteriormente generalizzabile. In fondo, l’angolo \(\gamma\) può essere scelto arbitrariamente, e, in generale, il segmento \(BD\) sarà di lunghezza \(\frac{x}{\tan\gamma}\). Viceversa, se il segmento \(DB\) è lungo \(\frac{x}{y}\), l’angolo \(\gamma\) sarà dato da \(\arctan y\).
Utilizza questa notazione per generalizzare la procedura che hai adottato sin qui, e, ricordando che
\[\beta = \pi – \arctan x – \arctan y,\]
ricava la formula
\[\arctan x + \arctan y = \pi – \arctan\left(\frac{x+y}{xy-1}\right),\]
valida per \(x > \frac{1}{y} >0.\)
