Nel risolvere problemi di geometria, mi è capitato più volte di cercare alternative tra un approccio trigonometrico e uno basato su congruenze e similitudini. Vi propongo il seguente esercizio, perché consente una maggiore gradualità nel passaggio da una strategia all’altra.
Sia \(\triangle ABC\) un triangolo in cui \(\angle BAC \cong 2 \angle ACB\), e sia \(D\) un punto su \(AC\) tale per cui \(\angle BAD \cong 2 \angle BAC\). Determinare la misura di \(\angle ABC\), sapendo che \[CD \cong 2BD+AD.\tag{1}\label{eq2950:1}\]
Soluzione 1 – Trigonometria “pura”
Quello che segue è una tecnica di “forza bruta”. Traduciamo la relazione tra segmenti \eqref{eq2950:1} in un’equazione nella sola incognita \(\angle ABC = \gamma\), e poi la risolviamo. Ecco come.
- Ottieni, dalla \eqref{eq2950:1}, l’equazione \[\frac{\overline{CD}}{\overline{BD}} =2 + \frac{\overline{AD}}{\overline{BD}}\tag{2}\label{eq2950:2}.\]
- Applica la regola dei seni a \(\triangle ADB\) e \(\triangle CDB\), ricavando così \[\frac{\overline{CD}}{\overline{BD}} = \frac{\sin 7 \gamma}{\sin \gamma}\] e \[\frac{\overline{AD}}{\overline{BD}}= \frac{\sin 4 \gamma}{\sin 2\gamma} .\]
- Ora l’equazione c’è, ma sfortunatamente non è semplicissima da risolvere: \begin{eqnarray}\frac{\sin 7 \gamma}{\sin \gamma} &=& 2 + \frac{\sin 4 \gamma}{\sin 2\gamma}\tag{3}\label{eq2950:3}. \end{eqnarray}
- La parte più convoluta è ricavare \(\sin 7 \gamma\) in funzione di \(\sin \gamma\). Con un po’ di pazienza, puoi farlo tu stesso, attraverso l’indentità \[\cos 7\gamma + i \sin7\gamma = (\cos \gamma + i \sin \gamma)^7\] e prendendo la parte immaginaria del secondo membro, dopo aver sviluppato la potenza. Dopo aver espresso il tutto in termini del solo seno ricaverai \[\sin 7\gamma = 7 \sin \gamma – 56 \sin^3\gamma + 112\sin^5\gamma-64\sin^7\gamma.\] Sostituisci quindi quanto ottenuto in \eqref{eq2950:3} per ricavare, dopo un ulteriore semplificazione, \[64\sin^6 \gamma – 112 \sin^4\gamma +52\sin^2\gamma-3 = 0.\]
- Usando il teorema delle radici razionali, fattorizza quindi il polinomio e ricava \[\left(4\sin^2\gamma-3\right)\left(16\sin^4\gamma-16\sin^2\gamma+1\right).\] Vincoli geometrici impongono che sia \(7\gamma<\pi\). Quindi l’unica soluzione valida si ottiene dal secondo fattore, ovvero\[\sin\gamma = \frac{\sqrt{2-\sqrt 3}}{2},\]that is \[\gamma = \frac{\pi}{12}.\]
Soluzione 2 – Congruenze preliminari
Partiamo da alcune costruzioni ausiliarie. Considera la Figura qui sotto, dove \(E\) è un punto su \(CD\) tale per cui \(ED\cong BD\). Inoltre \(AB\) è stato esteso fino al punto \(F\), in modo che sia \(AE\cong EF\).

Chiama per semplicità \(\angle BAC = \alpha\). Per ipotesi, quindi, abbiamo \(\angle ACB = \frac{\alpha}2\) e \(\angle ABD = 2\alpha\).
- Usa il Teorema dell’angolo esterno su \(\triangle ABD\) per esprimere l’angolo \(\angle EDB\) in funzione di \(\alpha\). Quindi, tenendo conto del fatto che \(\triangle BDE\) è isoscele, determina la misura degli altri suoi angoli interni.
- Usa l’ipotesi \eqref{eq2950:1} per dimostrare che \(AE\cong EC\).
- Considerando il cerchio circoscritto al triangolo \(\triangle ACF\), dimostra che \(\angle AFC= \frac{\pi}2\); da ciò consegue che \(\angle CEF = 2\alpha\).
- Usa i punti 1. e 3. per mostrare che sia \(\angle EBF\) che \(\angle BEF\) misurano \(\frac{\pi}2-\frac{\alpha}2\). Di conseguenza, \(BF\cong EF\). Deducine che\[\frac{\overline{BF}}{\overline{AC}} = \frac12.\]
- Trasforma la relazione precedente nell’equazione trigonometrica\[\sin \alpha \cot \frac{3\alpha}2 = \frac12.\]
- Usando le formule di somma, duplicazione e bisezione per seni e coseni, riscrivi l’equazione nella forma \[\frac{2\cos^2\frac{\alpha}2\left(2\cos \alpha -1\right)}{2\cos\alpha +1} = \frac12,\]e mostra che essa è equivalente a\[4\cos\alpha^2-3 = 0,\] la cui unica soluzione geometricamente valida è \(\alpha = \frac{\pi}6\).
Soluzione 3 – Geometria euclidea “pura”
L’approccio precedente ha permesso, attraverso l’uso di dimostrazioni preliminari, di semplificare l’equazione trigonometrica e quindi la sua soluzione.
Ma possiamo spingerci ancora oltre ed evitare la trigonometria del tutto! Allo scopo, aggiungiamo solo qualche altra linea al disegno precedente. Estendi \(CF\) fino a \(L\) così che \(CF\cong FL\). La situazione è riprodotta nella Figura sottostante.
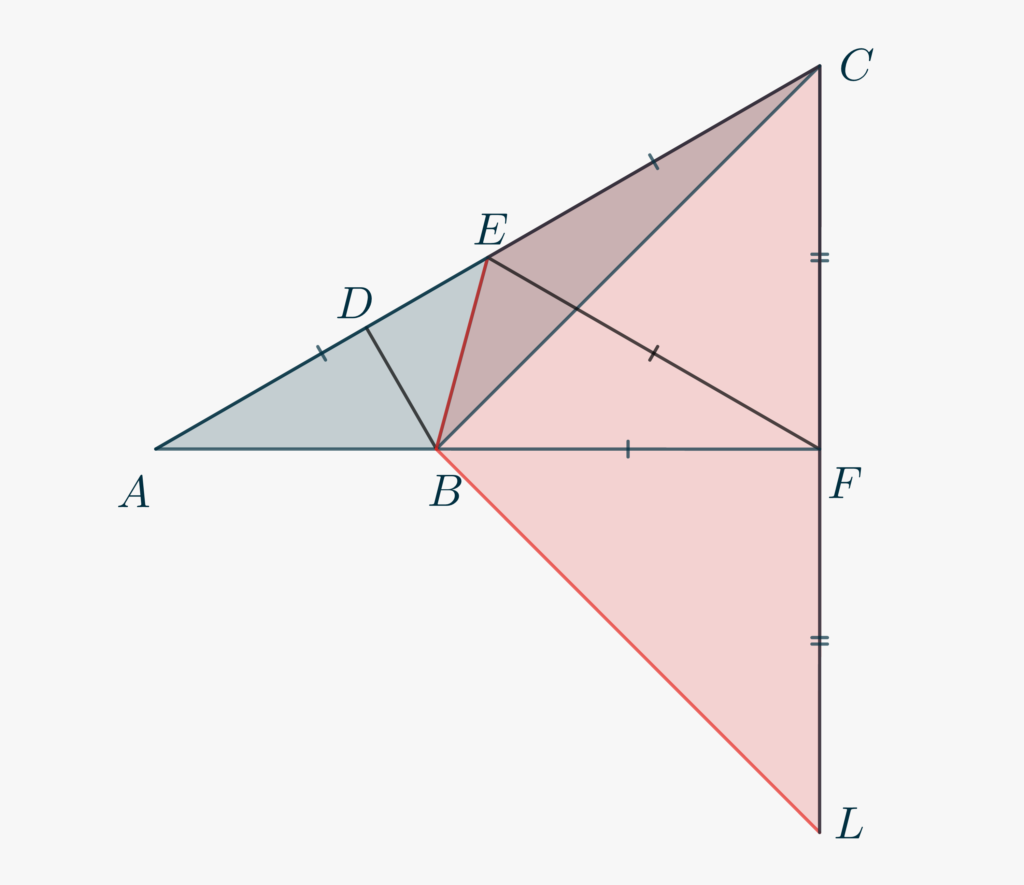
- Utilizzando le informazioni ottenute dai primi tre punti della Soluzione 2, recupera, nell’ordine, le seguenti relazioni: \[\angle BEC = \frac{\pi}2+\frac{3\alpha}2,\] \[\angle CBF = \frac{3\alpha}2,\]e\[\angle BCF = \frac{\pi}2-\frac{3\alpha}2.\]
- Dimostra, mediante il primo criterio di congruenza, che \(\triangle BCF \cong \triangle BFL\), e, in particolare, \(\angle BLF \cong \angle BCF\).
- Dai punti 1. e 2. deduci che il quadrilatero \(\square BLCE\) è circoscrivibile. Perché \(F\) è necessariamente il centro del cerchio in cui tale quadrilatero è inscritto?
- Deduci che il triangolo \(\triangle ECF\) è equilatero e perciò \(\alpha = \frac{\pi}6.\)
Di seguito un altro problema, con il quale puoi esercitarti ad usare questi differenti approcci.
In un triangolo \(\triangle ABC\), sia \(\angle ACB = 120^\circ\) e sia \(D\) un punto su \(AB\) tale per cui \(\angle ABC = 2\angle DCB\). Se \(AD \cong BC\) quanto misura l’angolo \(\angle DCB\)?
Suggerimenti. Per un approccio trigonometrico, prova a scrivere l’equazione \(AD = BC\) in termini di \(x = \angle DCB\). A questo scopo, usa la regola dei seni sui triangoli \(\triangle ADC\) e \(\triangle DBC\). Potrebbe essere utile ricordare che \(\sin\alpha\sin\beta = \frac12\left[\cos(\alpha-\beta)-\cos(\alpha+\beta)\right]\). Se vuoi seguire un approccio basato su congruenze, ad esempio, estendi \(AC\) dalla parte di \(C\), fino ad \(E\) in modo che \(AD\cong DE\), e considera i triangoli \(\triangle CDE\) e \(\triangle CBE\). Di che tipo di triangoli si tratta?\(\dots\) .