While solving some geometrical problems, I have been investigating on the possible alternatives between a trigonometric approach versus an approach based on congruences and similarities. I decided to show the following exercise, because it allows for a finer “tuning” between these two strategies.
Let \(\triangle ABC\) a triangle with \(\angle BAC \cong 2 \angle ACB\), and let \(D\) be a point on \(AC\) such that \(\angle BAD \cong 2 \angle BAC\). Determine the measure of \(\angle ABC\), knowing that \[CD \cong 2BD+AD.\tag{1}\label{eq2888:1}\]
Solution 1 – Fully trigonometric
This is a brute-force approach: we translate the given relationship between segments into a trigonometric equation, where \(\angle ABC = \gamma\) is the only unknown, and then solve it. Here’s how.
- Obtain, from \eqref{eq2888:1}, the equation \[\frac{\overline{CD}}{\overline{BD}} =2 + \frac{\overline{AD}}{\overline{BD}}\tag{2}\label{eq2888:2}.\]
- Apply the sine rule to \(\triangle ADB\) and \(\triangle CDB\) to obtain \[\frac{\overline{CD}}{\overline{BD}} = \frac{\sin 7 \gamma}{\sin \gamma}\] and \[\frac{\overline{AD}}{\overline{BD}}= \frac{\sin 4 \gamma}{\sin 2\gamma} .\]
- Now we have the equation, but, unluckily, it is one not quite easy to solve: \begin{eqnarray}\frac{\sin 7 \gamma}{\sin \gamma} &=& 2 + \frac{\sin 4 \gamma}{\sin 2\gamma}\tag{3}\label{eq2888:3}. \end{eqnarray}
- The cumbersome part is of course writing \(\sin 7 \gamma\) in terms of \(\sin \gamma\). You can do it yourself (it will take some time, mind you), using the identity \[\cos 7\gamma + i \sin7\gamma = (\cos \gamma + i \sin \gamma)^7\] and then taking the imaginary part of its RHS. After getting rid of all the cosine terms you will end up with \[\sin 7\gamma = 7 \sin \gamma – 56 \sin^3\gamma + 112\sin^5\gamma-64\sin^7\gamma.\] Replace this identity in \eqref{eq2888:3}, and after some further manipulation, obtain \[64\sin^6 \gamma – 112 \sin^4\gamma +52\sin^2\gamma-3 = 0.\]
- Use rational roots test to factor the equation into \[\left(4\sin^2\gamma-3\right)\left(16\sin^4\gamma-16\sin^2\gamma+1\right).\] Geometrical considerations force \(7\gamma<\pi\). So the only valid solution is obtained from the second factor, i.e.\[\sin\gamma = \frac{\sqrt{2-\sqrt 3}}{2},\]that is \[\gamma = \frac{\pi}{12}.\]
Solution 2 – Preliminary congruences
Let us start first with some additional constructions. Consider the Figure below, where \(E\) has been taken on \(CD\) so that \(ED\cong BD\). Also, \(AB\) has been produced to \(F\), in such a way that \(AE\cong EF\).

Call \(\angle BAC = \alpha\). Therefore, our hypotheses imply \(\angle ACB = \frac{\alpha}2\), and \(\angle ABD = 2\alpha\).
- Use External angle Theorem on \(\triangle ABD\) to determine, in terms of \(\alpha\), the angle \(\angle EDB\). Therefore, taking into account the fact that \(\triangle BDE\) is isosceles, determine its remainig internal angles.
- Use hypothesis \eqref{eq2888:1} to conclude that \(AE\cong EC\).
- By considering the circumcircle of \(\triangle ACF\), demonstrate that \(\angle AFC= \frac{\pi}2\), and therefore \(\angle CEF = 2\alpha\).
- Use 1. and 3. to show that both \(\angle EBF\) and \(\angle BEF\) have measure \(\frac{\pi}2-\frac{\alpha}2\). Thus \(BF\cong EF\). Show that the following equation holds true:\[\frac{\overline{BF}}{\overline{AC}} = \frac12.\]
- Translate the previous equation into the trigonometric equation\[\sin \alpha \cot \frac{3\alpha}2 = \frac12.\]
- Using addition and double-angle formulas for sine and cosine, rewrite the equation in the form \[\frac{2\cos^2\frac{\alpha}2\left(2\cos \alpha -1\right)}{2\cos\alpha +1} = \frac12,\]and show this to be equivalent to\[4\cos\alpha^2-3 = 0,\] whose only geometrically valid solution is of course \(\alpha = \frac{\pi}6\).
Solution 3 – Fully euclidean
The previous approach greatly simplified the trigonometric equation, and therefore its solution, by means of some preliminary use of Euclidean geometry theorems.
But we can push this strategy further, and completely avoid trigonometric equations! At this aim, let us start from the previous drawing and add just a few more lines. Produce \(CF\) to \(L\) so that \(CF\cong FL\). You will get to the picture shown below.
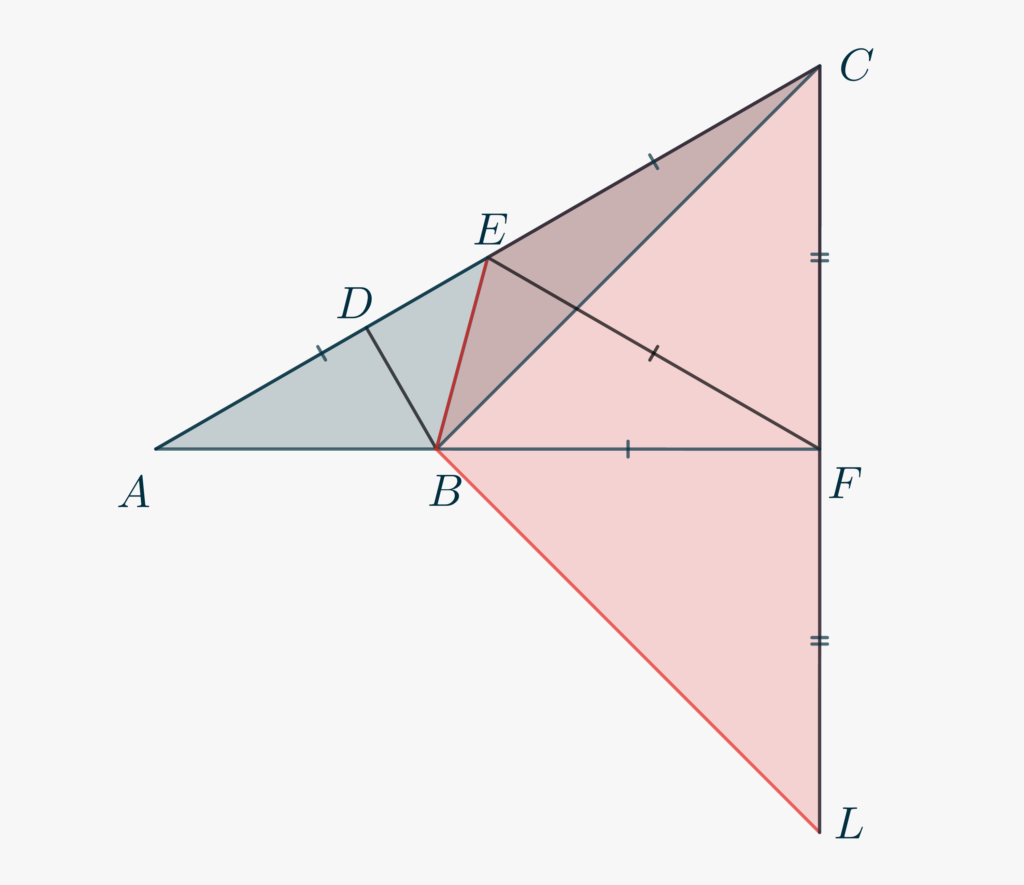
- By the previous angle chasing, recollect the following information: \[\angle BEC = \frac{\pi}2+\frac{3\alpha}2,\] \[\angle CBF = \frac{3\alpha}2,\]and\[\angle BCF = \frac{\pi}2-\frac{3\alpha}2.\]
- Use SAS criterion to get \(\triangle BCF \cong \triangle BFL\), and in particular \(\angle BLF \cong \angle BCF\).
- Use 1. and 2. to demonstrate that \(\square BLCE\) is cyclic. Why must \(F\) be the center of its circumscribed circle?
- Deduce that \(\triangle ECF\) is equilateral, and therefore \(\alpha = \frac{\pi}6.\)
Here is another exercise, for practicing these approaches.
In a triangle \(\triangle ABC\) let \(\angle ACB = 120^\circ\) and let \(D\) a point on \(AB\) such that \(\angle ABC = 2\angle DCB\). If \(AD \cong BC\) what is the measure of \(\angle DCB\)?
Hints. For a trigonometric approach, consider writing the equation \(AD = BC\) in terms of \(x = \angle DCB\). At this aim, use the sine rule on \(\triangle ADC\) and \(\triangle DBC\). It might be useful to recall that \(\sin\alpha\sin\beta = \frac12\left[\cos(\alpha-\beta)-\cos(\alpha+\beta)\right]\). For an euclidean approach, for example, produce \(AC\) to \(E\) so that \(AD\cong DE\), and consider triangles \(\triangle CDE\) and \(\triangle CBE\). What can you say about them?\(\dots\) .
