This is the first of a series of posts in which a problem is presented to the reader, who in invited to solve it by following a proposed path. The background knowledge required is mostly that of a second year high school student. The focus, in fact, is rather on finding simple and efficient solutions.
Given a square \(ABCD\), let \(E\), \(F\), and \(G\) be the midpoints of segments \(AD\), \(EC\), and \(BF\), respectively. Find the area of \(\triangle BDG\).
An accurate drawing is often a good starting point. While drawing, in fact, geometrical constraints might arise that can be of help once they are “translated” into algebraic expressions. For exampe, you may notice, in our case, the symmetrical position of point \(F\) with respect to sides \(AD\) and \(BC\) of the square. Too many lines, though, can be confusing.
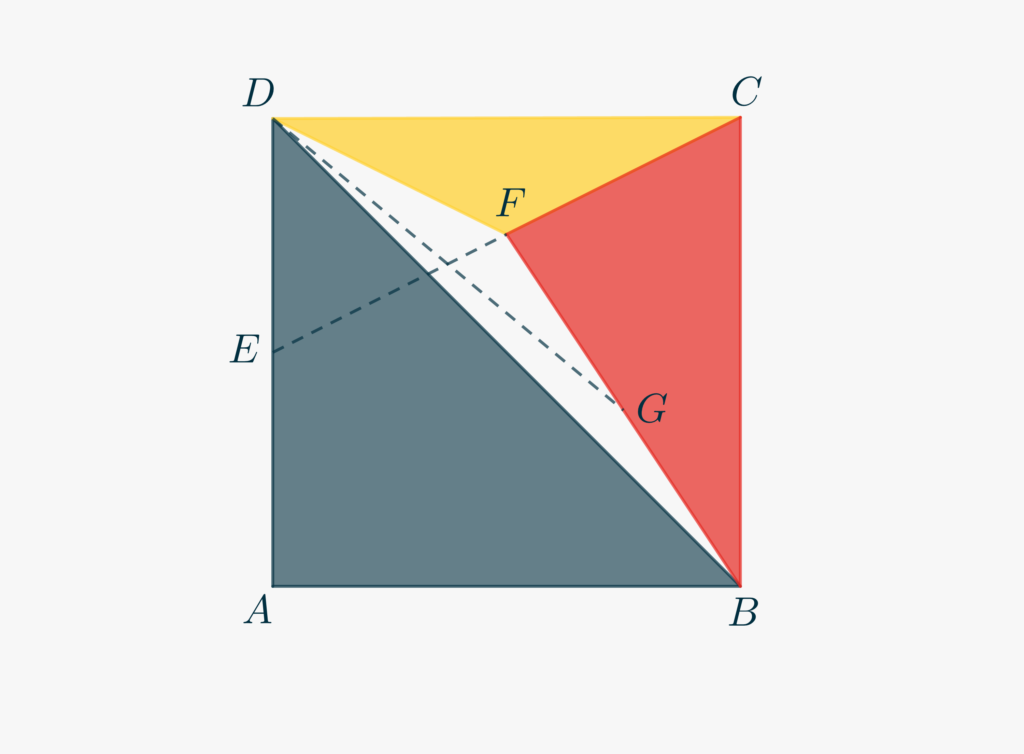
- Concentrate first on triangle \(\triangle BDF\) and note that \(DG\) is the median relative to side \(BF\).
- What is the relationship, then, between the area we want to calculate, i.e. that of \(\triangle BDG\), and the area of \(\triangle BDF\)?
- Thus, we can try to calculate the area of \(\triangle BDF\) and then divide by two to get our final result…
- Let us now go back to the symmetry of \(F\) and try to express it in mathematical terms. Draw from \(F\) the lines parallel to the square sides.
- Notice that the lines you just drew bisect \(EC\) and use Thales Theorem to determine the distance of \(F\) from \(BC\) and \(CD\).
- Using these results, you can now calculate the area of \(\triangle BDF\) by subracting, from the area of the square, that of three triangles. Which triangles? What are their areas?
- Finally divide by two to get \(\mathcal A_{BDG} = \frac{1}{16}\).
