C’è una qualche motivazione statistica che ci consente di confermare o smentire questo famoso detto?
Naturalmente, se lanciamo una moneta equilibrata e otteniamo due teste di fila, non abbiamo nessuna ragione per ritenere più probabile una terza testa anziché una croce.
Le cose cambiano, però, se non abbiamo informazioni riguardo alla moneta. In questo caso, occorre qualche altra assunzione riguardo alla probabilità di ottenere testa ad ogni lancio. Possiamo, ad esempio, supporre che la probabilità che il lancio dia testa, \(\mu\), abbia una distribuzione uniforme tra \(0\) e \(1\). Ora, sia \(X_k\) il numero di teste dopo i primi \(k\) lanci. La probabilità di ottenere tre teste, dato che i primi due lanci hanno dato entrambi testa è\[p=P(X_3=3 |X_2=2).\]Utilizzando il Teorema di Bayes, si ricava \begin{eqnarray}p &=& \frac{P(X_2=2|X_3=3)P(X_3=3)}{P(X_2=2)}=\\&=&\frac{P(X_3=3)}{P(X_2=2)},\tag{1}\label{eq3160:1}\end{eqnarray}dove abbiamo anche usato il fatto che \(P(X_2=2|X_3=3)\), cioè la probabilità di ottenere due teste di fila, dato che per tre lanci di fila si ottiene testa, è ovviamente \(1\).
Esplicitando il condizionamento rispetto a \(\mu\) porta a\[P(X_k=k|\mu) = \mu^k\]in modo che \eqref{eq3160:1} può essere riscritta come\begin{eqnarray}p&=&\frac{\int_0^1\mu^3 d\mu}{\int_0^1 \mu^2 d\mu}=\\&=&\frac{\left[\frac{\mu^4}{4}\right]_0^1}{\left[\frac{\mu^3}{3}\right]_0^1}=\frac34.\end{eqnarray}
Ovvero: se abbiamo ottenuto due teste di fila, è effettivamente più probabile (per la precisione, con una probabilità del \(75\)%) ottenere un’altra testa invece di una croce.
Analizziamo ora un caso simile, ma leggermente più complicato. Consideriamo un’urna che contiene in tutto \(m\) palline che possono essere bianche o nere. Non sappiamo, tuttavia, quale sia il numero di palline di ciascun colore. Supponiamo che i possibili numeri di palline bianche, ovvero \(0,1,2,\dots, m\) siano tutti equiprobabili (ovvero che il numero di palline bianche abbia una distribuzione uniforme discreta). Ipotizziamo, inoltre, di reinserire ogni volta nell’urna la pallina via via estratta. Se estraiamo due volte di fila una pallina bianca, qual è la probabilità che anche la terza pallina sia bianca? Puoi ottenere il risultato seguendo il percorso qui sotto indicato.
- Usa la stessa notazione dell’esercizio precedente, indicando questa volta con \(X_k\) il numero di palline bianche estratte dall’urna dopo la \(k\)-esima estrazione. Ancora una volta mediante il Teorema di Bayes otterrai che la probabilità richiesta si può scrivere come\[p=\frac{P(X_3=3)}{P(X_2=2)}.\]
- Osserva che la probabilità di ottenere una pallina bianca, condizionata al numero \(j\) di palline bianche contenute nell’urna, in ogni estrazione è uguale a \(\frac{j}{m}\), con\(j=1,2,\dots,m\).
- Usa 2. e l’indipendenza tra un’estrazione e l’altra, insieme all’ipotesi di distribuzione uniforme per \(j\), in modo da riscrivere \(p\) come\[p=\frac{\sum_{j=1}^m\left(\frac{j}{m}\right)^3}{\sum_{j=1}^m\left(\frac{j}{m}\right)^2}.\]
- Infine usa i risulati noti \[\sum_{j=1}^m j^2 = \frac{m(m+1)(2m+1)}6,\] e \[\sum_{j=1}^m j^3 = \frac{m^2(m+1)^2}4\] per ricavare \[p=\frac{3(m+1)}{2(2m+1)}.\]
Il risultato, in questo caso, dipende dal numero di palline nell’urna, \(m\). Se \(m=1\), il fatto di aver estratto per due volte una pallina bianca implica che l’unica pallina nell’urna è bianca, per cui, naturalmente, \(p=1\). Inoltre, quando \(m\to \infty\) si ha \[p\to \frac34,\]come mostra il grafico qui sotto, che rappresenta la funzione \(f(x) = \frac{3(x+1)}{2(2x+1)}\), per \(x\geq 1\), insieme al suo asintoto orizzontale.
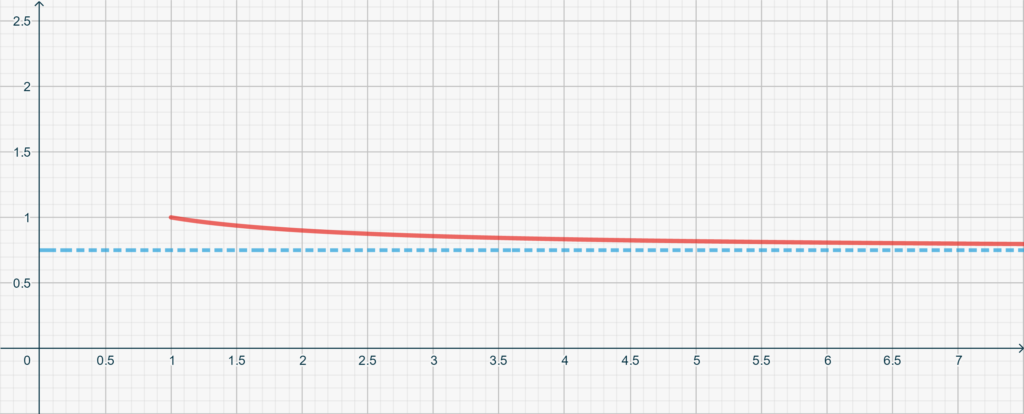
Per ogni valore di \(m\) abbiamo comunque \(p> \frac34\), il che conferma, anche in questo caso, che, se abbiamo estratto due palline bianche, è più probabile che la terza estratta sia anch’essa bianca.
Supponiamo ora che l’urna contenga almeno \(3\) palline, e di non reinserire nell’urna le palline di volta in volta estratte. In questo caso i calcoli sono più articolati, ma il risultato è sorprendentemente semplice.
- Esprimi di nuovo la probabilità richiesta come \(p=\frac{P(X_3=3)}{P(X_2=2)}\).
- Condizionando al numero \(j\) di palline bianche nell’urna, ora ci dà\[P(X_2=2|j) = \frac{j(j-1)}{m(m-1)}, \ \ j=1,2,\dots,m.\]
- Ricava, similmente, \[P(X_3=3|j) = \frac{j(j-1)(j-2)}{m(m-1)(m-2)}, \ \ j=2,3,\dots,m.\]
- Usando i risultati appena ottenuti, ricava\begin{eqnarray}p&=&\frac{\sum_{k=0}^{m-3}\frac{(m-k)(m-k-1)(m-k-2)}{m(m-1)(m-2)}}{\sum_{k=0}^{m-2}\frac{(m-k)(m-k-1)}{m(m-1)}}=\\&=&\frac1{m-2}\cdot\frac{\sum_{k=0}^{m-3}(m-k)(m-k-1)(m-k-2)}{\sum_{k=0}^{m-2}(m-k)(m-k-1)}=\\&=&\frac1{m-2}\cdot \frac{\mathcal N(m)}{\mathcal D(m)}.\end{eqnarray}
- Dimostra, per induzione, che \begin{eqnarray}\mathcal N(m) &= &\sum_{k=0}^{m-3}(m-k)(m-k-1)(m-k-2)=\\&=&\frac{(m-2)(m-1)m(m+1)}4, \ \ m=3,4,\dots,\end{eqnarray}e che\begin{eqnarray}\mathcal D(m) &= &\sum_{k=0}^{m-2}(m-k)(m-k-1)=\\&=&\frac{(m-1)m(m+1)}3, \ \ m=2,3,\dots.\end{eqnarray}
- Concludi che \[p=\frac34,\]indipendentemente dal numero di palline contenute nell’urna, purché, ovviamente, sia maggiore di \(2\).
Come ulteriore esercizio, ti propongo di generalizzare il risultato ottenuto qui sopra, determinando la probabilità di ottenere \(t\) palline bianche in \(t\) estrazioni successive, dato che le prime \(t-1\) estrazioni hanno dato soltanto palline bianche.
