In this post the behavior of sequences obtained by convolving two sequences is analyzed. In particular, we will give sufficient conditions for the convolution to be a null sequence.
Given two sequences \(a_n\) and \(x_n\), \(n=0,1,2\dots\), we define their convolution as the sum of the product between each element of one sequence and the corresponding element of a “reversed” and “shifted” version of the other one. Therefore we have
\[y_n = \sum_{k=0}^n a_{n-k}x_k.\]
We will demonstrate the following.
Theorem. Let \((x_n)\), \(n=0,1,2,\dots\) be a null sequence and \(\sum_{k=0}^{+\infty}a_n\) an absolutely converging series. Then the sequence \((y_n)\) defined by
\[y_n = \sum_{k=0}^n a_{n-k}x_k\]
is a null sequence.
Suppose \(\left(\sum |a_n|\right) \to L\). Fix \(\varepsilon>0\) and choose \(N_1\) so that, for \(n>N_1\)
\[|x_n| < \frac{\varepsilon}{2L}.\]
Also recall that, being a converging sequence, \((x_n)\) is bounded, i.e. there exists a postive \(M\) such that
\[|x_n|<M\]
for all \(n\).
Now, using triangular inequality yields
\begin{eqnarray}\left|y_n\right| &=&\left| \sum_{k=0}^n a_{n-k}x_k\right|\leq\\&\leq&\left|\sum_{k=0}^{N_1}a_{n-k}x_k\right| + \left|\sum_{k=N_1+1}^n a_{n-k}x_k\right| \leq \\&\leq&\sum_{k=0}^{N_1}\left|a_{n-k}\right|\cdot \left|x_k\right| + \sum_{k=N_1+1}^n\left| a_{n-k}\right|\cdot\left|x_k\right|<\\&<&M\sum_{k=n-N_1}^{n}\left|a_{k}\right| + \frac{\varepsilon}{2L}\sum_{k=0}^{n-N_1-1}\left| a_{k}\right|\tag{1}\label{eq2845:1}.\end{eqnarray}
Absolute convergence gives us that
\[\sum_{k=0}^{n-N_1-1}|a_k| < L\]
for all \(n\). Cauchy criterion yields
\[\sum_{k=n-N_1}^n|a_k|<\frac{\varepsilon}{2M},\]
for \(n>N_2\). From \eqref{eq2845:1}, with \(n>N_2\), we get
\begin{eqnarray}|y_n| &<& M\frac{\varepsilon}{2M} + \frac{\varepsilon}{2L} L =\\&=& \varepsilon.\end{eqnarray}
\(\blacksquare\)
As an exercise, I propose you to demonstrate that the sequence recursively defined as
\[y_{n+1} = \frac{n}{n+1}+\frac23 \cdot y_n,\ \ n=0,1,2\dots,\]
with \(y_0\) any real quantity, converges to \(3\). Below you see the plot of the sequences having initial value \(y_0 = -3, 1, 10\), respectively.
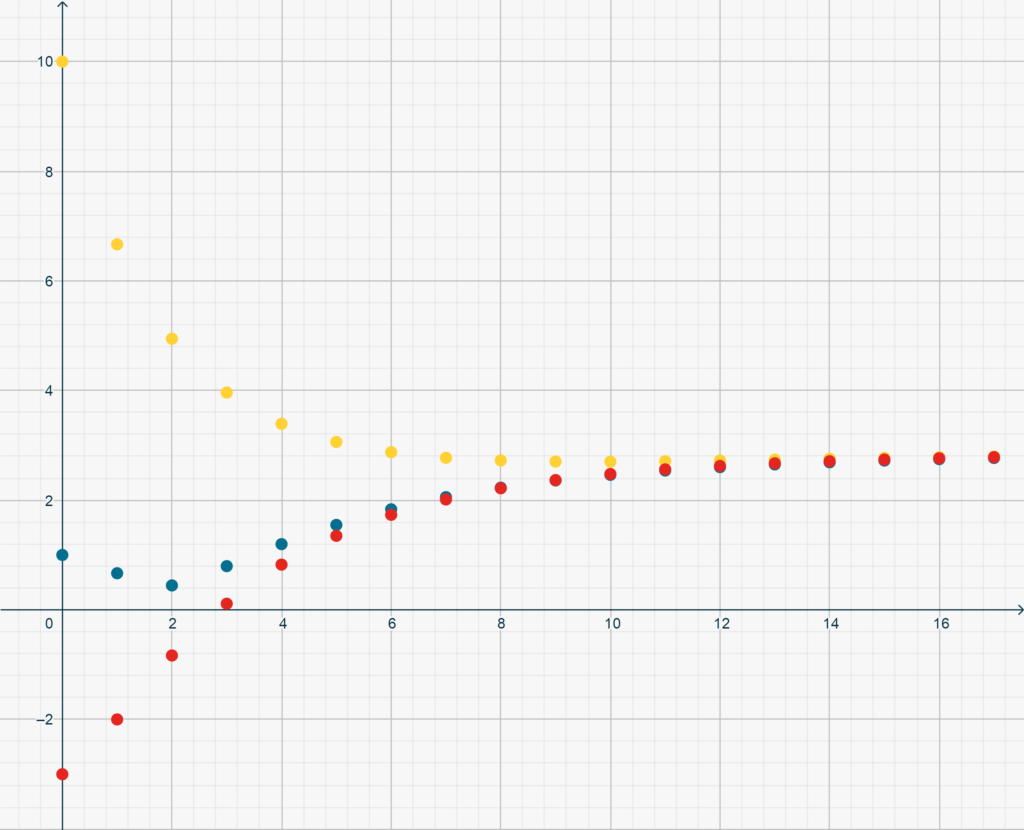
Hint. Rewrite the recursion using the variable \(z_n = y_n-3\). Express \(z_{n}\) as \[z_{n} = \sum_{k=0}^n\left(\frac23\right)^{n-k}x_k,\]with \[x_n =\begin{cases} z_0 & (n=0)\\-\frac1{n+1} & (n>0),\end{cases}\]and then make use of the above Theorem to show that \((z_n) \to 0\).
