Monotonia e continuità sono concetti molto diversi tra loro. Tuttavia, se consideriamo una funzione monotona che ha come dominio un intervallo reale, siamo certi che la funzione ammetterà limiti destro e sinistro (eventualmente diversi) in ogni punto dell’intervallo. Questa è una conseguenza dell’assioma di Completezza, in base al quale ogni insieme limitato superiormente (inferiormente) ammette estremo superiore (inferiore).
Possiamo allora dimostrare, per le funzioni monotone, un Teorema che ricorda il Teorema dei Valori Intermedi, pur essendo, ovviamente, più ‘debole’.
Teorema
Teorema Sia \(f:[0,1]\rightarrow [0,1]\) una funzione monotona non decrescente. Allora esiste un punto \(\alpha \in [0,1]\) tale per cui \(f(\alpha) = \alpha\).
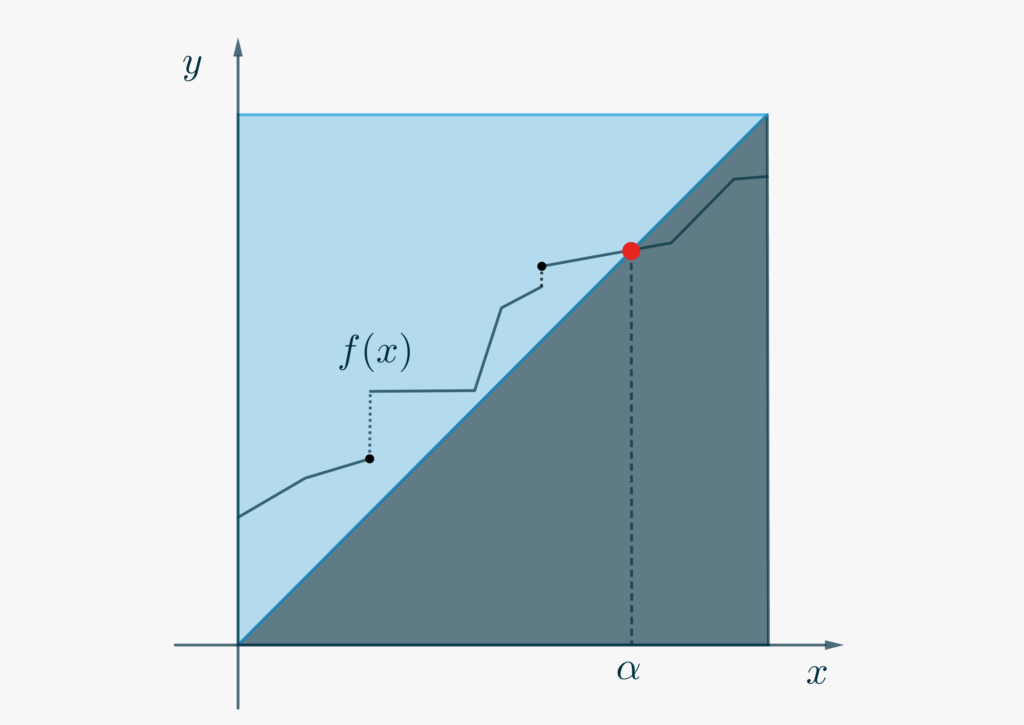
Dimostrazione
Anche la dimostrazione ricorda molto quella del Teorema dei Valori Intermedi.
Se \(f(0) = 0\) oppure \(f(1)=1\), allora abbiamo trovato il punto \(\alpha\). Altrimenti costruiamo due sequenze che si interrompono nel punto cercato oppure convergono ad esso. Vediamo come.
Fissiamo \(a_0 = f(0)\) e \(b_0=f(1)\); poi, per \(n=1,2,3,\dots\) procediamo così.
- Calcoliamo \(x_n = \frac{a_{n-1}+b_{n-1}}{2}\);
- Se \(f(x_n) = x_n\) allora \(\alpha = x_n\) e la ricerca ha termine;
- Se \(f(x_n) > x_n\) allora poniamo \(a_n = x_n\) e \(b_n = b_{n-1}\);
- Se \(f(x_n) < x_n\) allora poniamo \(a_n = a_{n-1}\) e \(b_n = x_n\).
Verifichiamo ora che, se la ricerca non si interrompe, le due successioni \((a_n)\) e \((b_n)\) convergono al valore desiderato. Anzitutto queste successioni sono monotone e limitate, quindi convergono (ed è qui che la Completezza entra in gioco). Dal momento che
\[a_n-b_n = \frac{1}{2^n},\]
esse convergono allo stesso numero \(\overline{x}\).
Inoltre abbiamo
\begin{equation}f(a_n)>a_n\tag{1}\label{eq335:a}\end{equation} e
\begin{equation}f(b_n)< b_n\tag{2}\label{eq335:b}\end{equation}
per ogni \(n\).
Supponiamo sia \(f(\overline{x}) < \overline x\). Allora, per la convergenza di \((a_n)\) a \(\overline x\), avremo, per \(n\) abbastanza elevato,
\[f(\overline x) < a_n < \overline x.\]
Tuttavia, ciò, insieme con la \eqref{eq335:a}, implica \(f(a_n) > f(\overline x)\), in contraddizione con la monotonia di \(f(x)\). Analogamente, se fosse \(f(\overline x) > \overline x\), per la convergenza di \((b_n)\) a \(\overline x \), si avrebbe, con \(n\) sufficientemente grande,
\[\overline x < b_n < f(\overline x).\]
Ma la \eqref{eq335:b} implica allora \(f(b_n) < f(\overline x)\), che, ancora un volta, non è compatibile con la monotonia della funzione. Quindi deve essere \(f(\overline x) = \overline x\). Dunque \(\overline x = \alpha\) è il valore cercato.
Per concludere, osserva che la completezza è, in effetti, necessaria affinché il Teorema sia vero. Ad esempio prendiamo la funzione \(f: [0,1]\cap\Bbb Q \rightarrow [0,1]\cap\Bbb Q\)
\[f(x) = \frac{1}{3-x},\]
che è monotona e continua nel suo dominio. In questo caso non esiste alcun \(\alpha\) tale per cui
\[\frac{1}{3-\alpha} = \alpha,\]
perché \(\alpha\) sarebbe soluzione dell’equazione
\[\alpha^2-3\alpha + 1 = 0,\]
che però non ammette soluzioni in \(\Bbb Q\).
Come ulteriore esercizio puoi provare a dimostrare nuovamente il Teorema dopo aver sostituito “monotona non decrescente” con “continua”. (Suggerimento: utilizza la funzione ausiliaria \(F(x) = f(x) – x\).)
