Teorema. Sia \(f\) una funzione reale, derivabile fino all’ordine \(n\) in \(c \in \Bbb R\), per un qualche intero positivo \(n\). Si supponga che \(f^{(n)}(c) \neq 0\), e che tutte le derivate di ordine inferiore (se presenti) siano nulle in \(c\). Allora \(c\) è un punto estremante se e solo se \(n\) è pari.
Nel seguito useremo la notazione \(f^{(k)}(x)\), con \(k>0\) per indicare la derivata di ordine \(k\) di \(f\) in \(x\); per \(k=0\), \(f^{(0)}(x) = f(x)\). Assumeremo inoltre, senza perdita di generalità, che \(c=0\), \(f(0)=0\), e \(f^{(n)}(0)>0\).
Avendo informazioni sulla derivata di ordine \(n\) in \(c\) ma non in un intorno di \(c\), non possiamo utilizzare lo sviluppo di Taylor. Questo è il motivo per cui ho deciso di proporre questo teorema e la sua dimostrazione. Se tuttavia utilizziamo la classica definizione di derivata, come fornita ad esempio in “Principles of Mathematical Analysis” di W. Rudin (def. 5.1, pagina 103), per \(k=1,2,\dots\), l’esistenza di \(f^{(k)}(c)\) implica l’esistenza di \(f^{(k-1)}(x)\) in tutto un intervallo che contiene \(c\). Il che ci permetterà di fare uso del Teorema di Lagrange.
Per prima cosa osserviamo che \[\lim_{x\to 0}\frac{f^{(n-1)}(x)}{x} = f^{(n)}(0) > 0,\]da cui deduciamo l’esistenza di un intorno \(\mathcal N\) of \(0\) tale per cui \[\frac{f^{(n-1)}(x)}{x} > 0,\tag{1}\label{eq3769:1}\]per ogni \(x \in \mathcal N\setminus \{0\}\). Se \(n=1\) la dimostrazione è conclusa, dal momento che dalla \eqref{eq3769:1} \(f^{(0)}(x)=f(x)\) segue che la \(f\) non ha massimo o minimo locale in \(0\).
Se \(n>1\), dalla \eqref{eq3769:1} possiamo concludere che \[f^{(n-2)}(x)>0\tag{2}\label{eq3769:2}\] per ogni \(x\in \mathcal N\setminus \{0\}\). Possiamo dimostrare ciò per assurdo. Supponiamo infatti esista \(\overline x \in \mathcal N\setminus \{0\}\) tale per cui \(f^{(n-2)}(\overline x)\leq 0\). Allora, per il Teorema di Lagrange dovrebbe esistere \(\xi\) tale per cui \[f^{(n-1)}(\xi) = \frac{f^{(n-2)}(\overline x)}{\overline x}.\] Se \(\overline x >0\), allora \(0< \xi <\overline x\) e \(f^{(n-1)}(\xi) \leq 0\). Se, invece, \(\overline x < 0\), allora \(\overline x < \xi < 0\) e \(f^{(n-1)}(\xi) \geq 0\). Entrambe le situazioni contraddicono l’equazione \eqref{eq3769:1}.
Se \(n=2\) abbiamo nuovamente raggiunto la tesi, dal momento che dall’equazione \eqref{eq3769:2} segue che \(0\) è un minimo locale (il che dipende dalla scelta che abbiamo fatto, di porre \(f^{(n)}(0) > 0\)).
Se \(n>2\), osserva che \eqref{eq3769:2} implica che \(f^{(n-3)}(x)\) è strettamente monotona in \(\mathcal N\). Insieme all’ipotesi \(f^{(n-3)}(0) = 0\), questo implica \[\frac{f^{(n-3)}(x)}{x} > 0\]per ogni \(x \in \mathcal N \setminus \{0\}\).
A questo punto è immediato procedere iterativamente e mostrare che \[f^{(n-2k)}(x)>0 \ \ \mbox{per} \ \ k=0,1\dots ,\left\lfloor \frac{n}2\right\rfloor-1\] per ogni \(x \in \mathcal N \setminus \{0\}\), e che \[\frac{f^{(n-2k-1)}(x)}{x} > 0\ \ \mbox{per} \ \ k=0,1,\dots ,\left\lfloor \frac{n}2\right\rfloor-1\] per ogni \(x \in \mathcal N \setminus \{0\}\). La tesi consegue da queste due ultime equazioni.
Ecco alcuni interessanti esempi. Il primo è estratto da “Numbers and Functions” di Robert Burn. Considera\[f(x) = \begin{cases}x + 2x^2 \cos\left(\frac1{x}\right) & (x\neq 0) \\ 0 & (x=0).\end{cases}\] Questa funzione ha la derivata prima in \(0\) uguale a \(1\) (usa la definizione di derivata!). Tuttavia \(f(x)\) non è crescente in alcun intorno di \(0\). Per esercizio puoi dimostrare infatti che \(f\left(\frac1{2k\pi}\right) > f\left(\frac1{(2k-1)\pi}\right)\) per ogni \(k =1,2,\dots\). Osserva infine che \(f'(x)\) non è continua in \(0\).
L’esempio precedente può essere generalizzato usando la funzione\[f(x) = \begin{cases}\frac{ax^n} {n!} + x^{2n}\cos\left(\frac1{x}\right) & (x\neq 0)\\ 0 & (x=0),\end{cases}\]dove \(f^{(k)}(0) = 0\) per \(0<k<n\) e \(f^{(n)}(0) = a\), con \(f^{(n)}(x)\) non continua in \(0\).
Nota che l’enunciato del Teorema richiede che esista almeno una derivata non nulla.
Se tutte le derivate in \(c\) fino all’ordine \(n-1\) esistono e sono uguali a \(0\), e la derivata \(n\)-esima in \(c\) non esiste, non si può trarre alcuna conclusione sull’esistenza o meno di un massimo/minimo locale. Considera ad esempio \[f(x) = \begin{cases} x^{2(n-1)}\left[2 + \cos \left(\frac1{x}\right)\right] & (x\neq 0) \\ 0 & (x=0). \end{cases}\tag{3}\label{eq3769:3}\]Questa funzione, per ogni \(n>1\), ha un minimo (globale) in \(0\), ha derivata \(k\)-esima \(f^{(k)}(0) = 0\) per \(0<k<n\), mentre \(f^{(n)} (x)\) non è definita in \(0\) (vedi figura qui sotto).
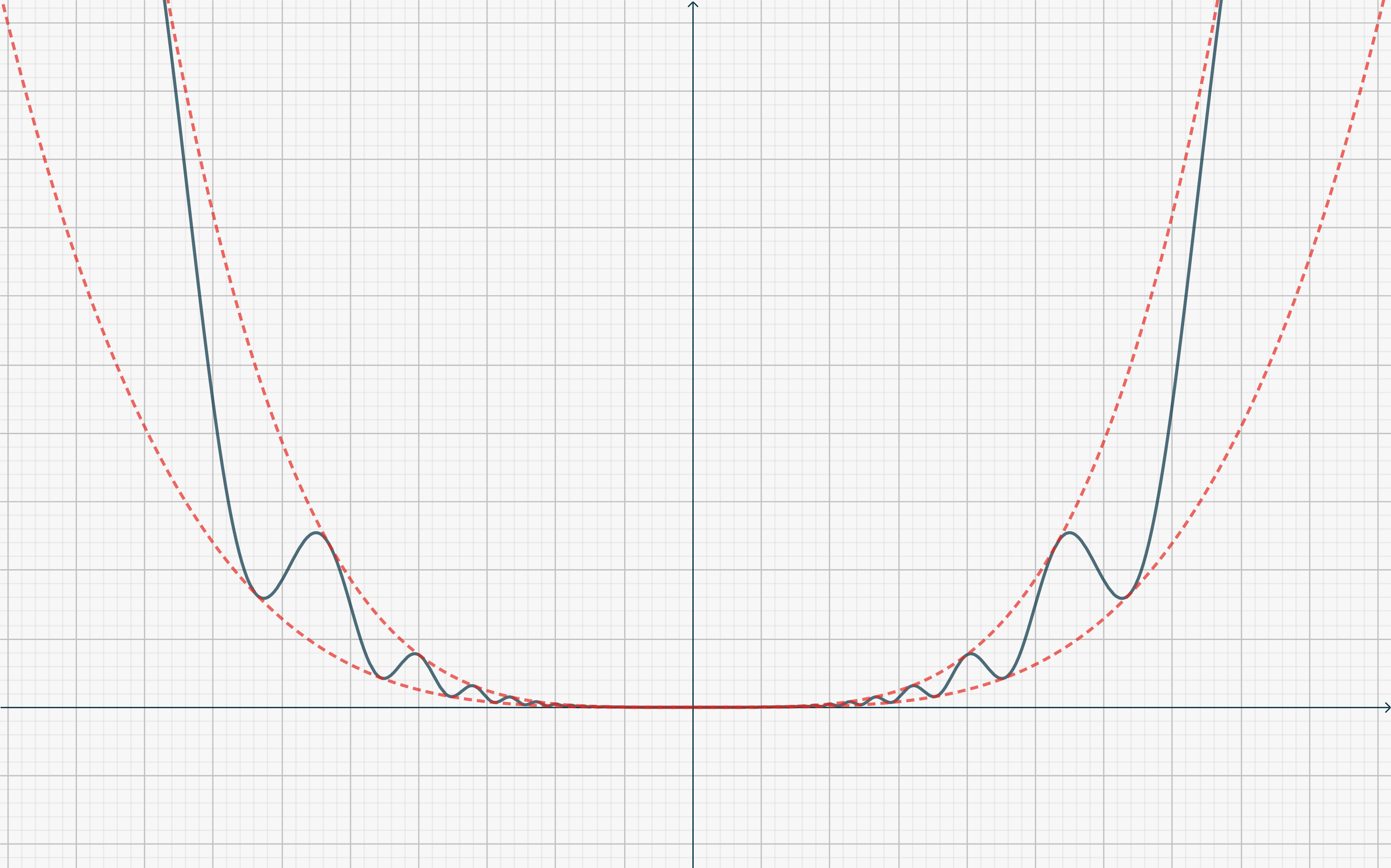
Esercizio proposto.
- Mostra che, per \(x \neq 0\), la derivata della funzione \eqref{eq3769:3} può essere maggiorata come segue.\[f'(x) \leq x^{2n-4}\sin\left(\frac1{x}\right) + 6(n-1)x^{2n-3}.\]
- Deduci che per \(x = \frac1{2k\pi -\frac{\pi}2}\), con \(k\) intero e \(k>\frac14 + \frac{3(n-1)}{\pi}\), \(f'(x)\) è negativa.
- Concludi che \(f(x)\) non è monotona crescente in alcun intorno destro di \(0\).
In modo analogo, per \(n>1\), la funzione\[f(x) = \begin{cases} x^{2n-1}\left[2 + \cos \left(\frac1{x}\right)\right] & (x\neq 0) \\ 0 & (x=0). \end{cases}\] (che non ha un punto di massimo o minimo in \(0\), essendo una funzione dispari) ha derivate nulle (e continue) in \(0\) fino all’ordine \(n-1\), mentre la derivata \(n\)-esima in \(0\) non esiste. La situazione è schematizzata dalla Figura qui sotto.
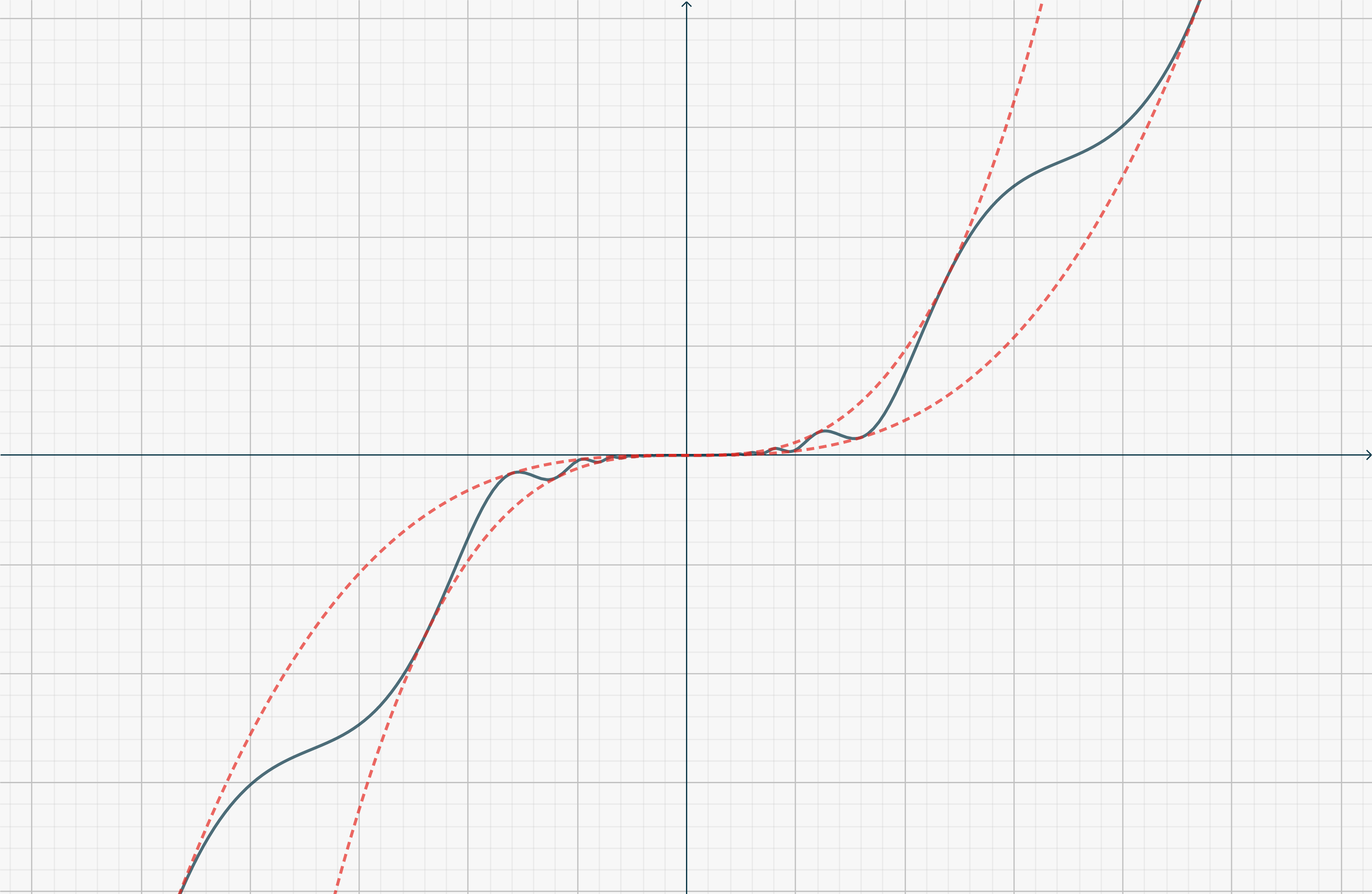
Per ragioni simili, se tutte le derivate sono nulle in \(c\) non si può trarre alcuna conclusione. Considera ad esempio\[f(x) = \begin{cases} e^{-\frac1{x^2}} & (x\neq 0) \\ 0 & (x=0),\end{cases}\]e\[f(x) = \begin{cases} \frac{x}{|x|}e^{-\frac1{x^2}} & (x\neq 0) \\ 0 & (x=0).\end{cases}\]